Der lange Weg zu unserem Musiksystem (Folge 1)
Liebe Leserinnen und Leser, wer Klavier, Pianoakkordeon oder Synthesizer spielt hat täglich mit dem Tonsystem zu tun, das die Tastatur uns präsentiert: In jeder Oktave sieben weiße und fünf schwarze Tasten.
Text: Peter M. Haas
Weiß und schwarz
„Die schwarzen Rippchen sind für traurige Musik“, sagt der beschwipste Onkel Otto, der keine Ahnung hat. Anfänger sind erst einmal erschrocken, wenn sie zu viele „schwarze Rippchen“ benutzen müssen. Wer weitergekommen ist, freut sich, dass – zum Beispiel in romantischer Klaviermusik – durch die vielen schwarzen Tasten das Übersetzen in brillanten Läufen viel leichter fällt.
Faszinierende Logik
Tatsächlich ist unser System der Töne und Tonleitern faszinierend logisch aufgebaut. Die Mehrzahl meiner Leser werden es wissen:
Von C ausgehend reiht sich – jeweils eine Quinte höher – die Folge der Tonleitern, die Kreuze benötigen: erst eines, dann zwei, dann drei …
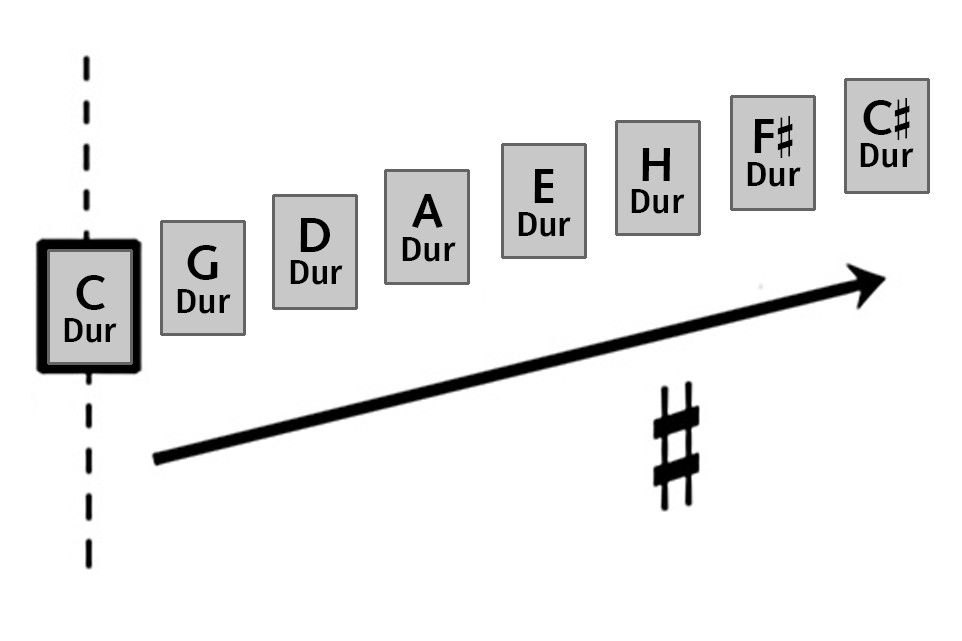
teihe-#-NEU
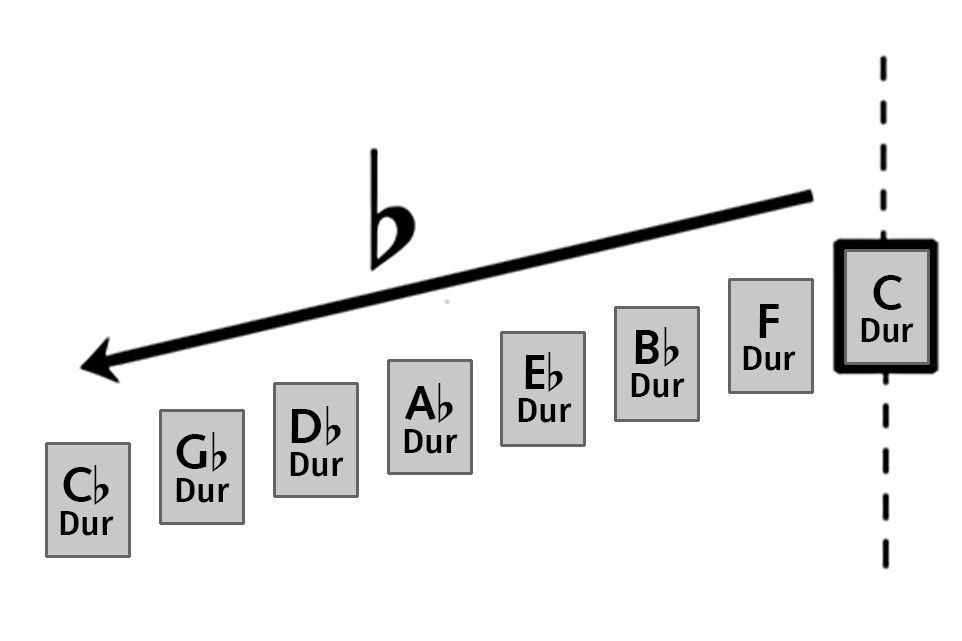
reihe-b-NEU
Diese lange Reihe der Tonleitern (siehe obere der beiden Abb.) kann ich zum Kreis schließen (Abb. darunter), denn ich darf ja h = ces, fis = ges, des = cis gleichsetzen. (Das ist die sogenannte enharmonische Verwechslung).
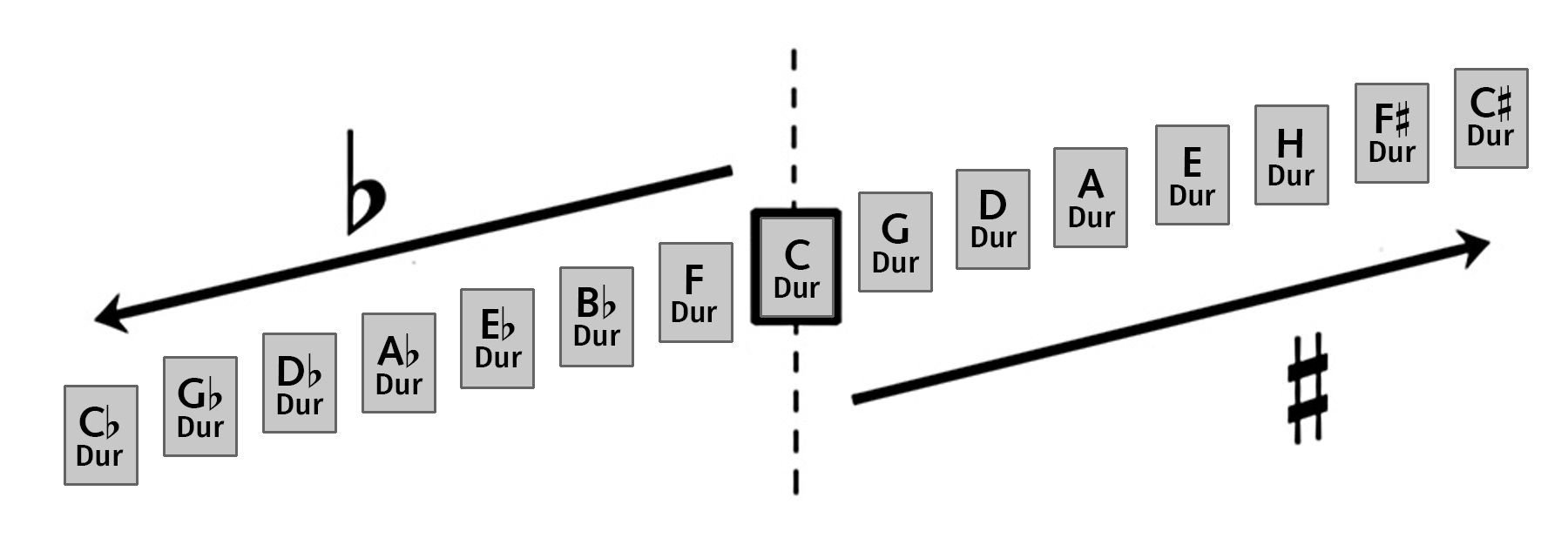
Quintenreihe NEU
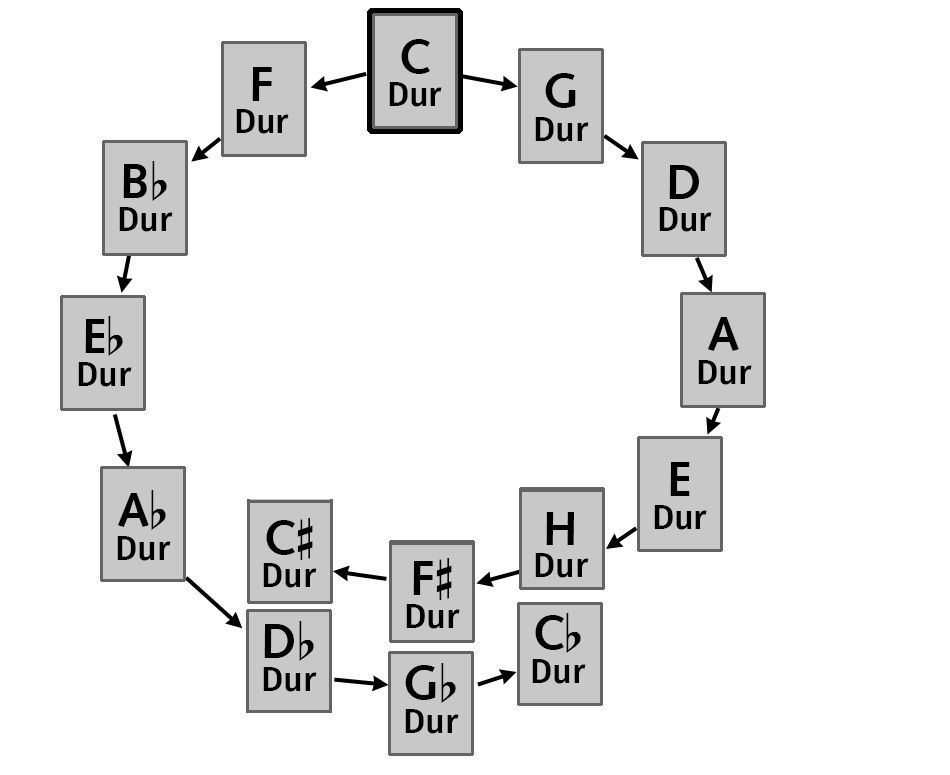
Quintenkreis-NEU
So ist ein Kreis entstanden, der alle Töne sowie ihre Tonleitern und Akkorde enthält und in dem ich mich als Komponist – mit Tonart- und Akkordwechseln – frei bewegen kann. Ohne die geniale Logik dieses Kreises wäre die Musikgeschichte auf dem Stand der Renaissance stehen geblieben; alle Effekte der komponierten Musik im 19. und 20. Jahrhundert beruhen auf dieser Bewegungsfreiheit.
Die Ernüchterung: diese Fakten sind gefälscht.
Sie stimmen nicht – jedenfalls wenn man die natürlichen Schwingungsverhältnisse der Töne zu Grunde legt. Hinter dem System, das uns auf dem Tasteninstrument die Freiheit zwischen allen Tonarten ermöglicht, steckt Betrug. Unsere moderne Stimmung beruht auf einer groß angelegten Fälschungsmaßnahme der Klavierbauer und Musiktheoretiker.
Warum und wie genau – das werden wir im weiteren Verlauf dieses Beitrags entdecken.
Einige Grundbegriffe
Bevor ich Weiteres erkläre, muss ich ein paar Grundbegriffe über Tonhöhen, Frequenzen und Frequenzverhältnisse klären.
Frequenz und Oktave
Die Höhe eines Tones wird durch die Schwingungszahl bestimmt, die sogenannte Frequenz des Tones. Der Stimmton a‘ rechts von der Klaviermitte hat beispielsweise eine Frequenz von 440 Hertz.
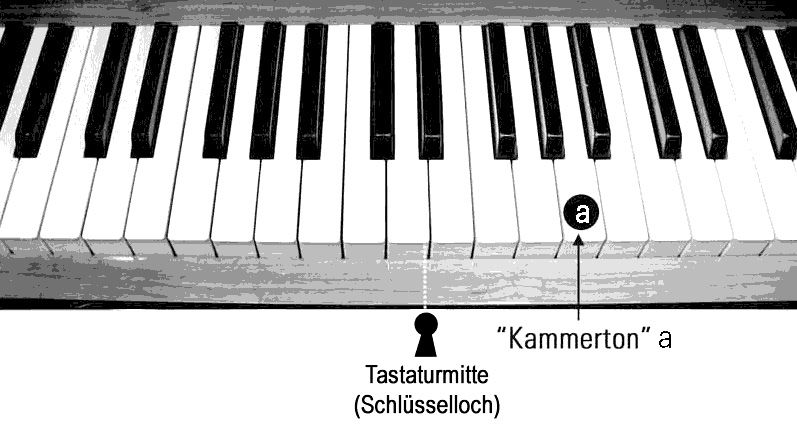
02kammerton
Die doppelte Frequenz ergibt den Ton, der eine Oktave höher ist. Für jeden beliebigen Ton mit der Frequenz F hat also seine Oktave die doppelte Frequenz, also zweimal F.
Etwa für den Ton C
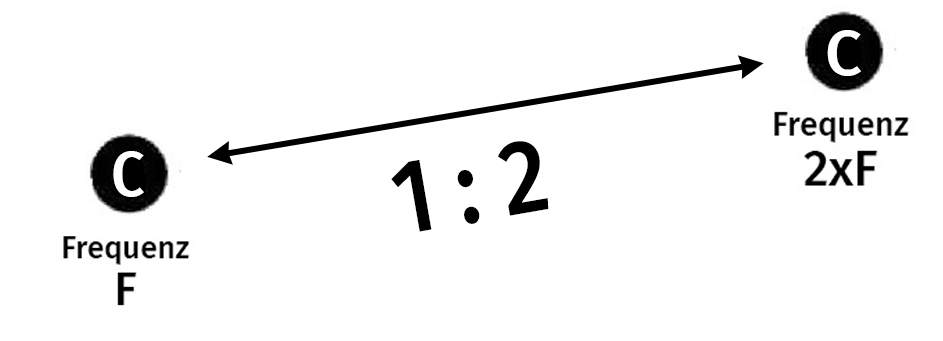
Oktave 1 - 2
Um die Frequenzen der chromatischen Tonkette c – cis – d – dis – e … bis zum nächsten c zu ermitteln, gab es im Laufe der Geschichte viele Berechnungsmodelle. Mit der gleichschwebenden Stimmung wurde mit allen Feinheiten kurzer Prozess gemacht, und man rang sich dazu durch, die Oktave in zwölf gleiche Schritte aufzuteilen.
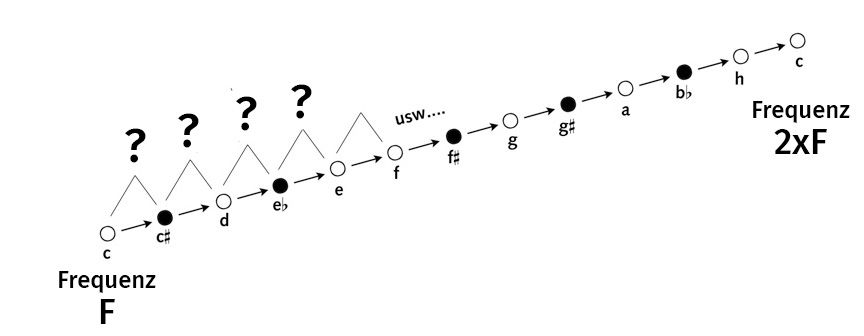
c bis c welcher Faktor_
Welche Zahl muss bzw. kann ich zwölfmal als Faktor setzen, um am Ende der Oktavkette bei der neuen, doppelten Frequenz 2 × F anzukommen? (Ups – allzu gut war ich früher selbst nicht in Algebra!) Aber tatsächlich ist der gesuchte Faktor die zwölfte Wurzel aus zwei. Als Zahlenwert ist das (auf drei Stellen gerundet) die Zahl 1,059.
Heureka – so viel misst in der modernen Stimmung ein Halbtonschritt!
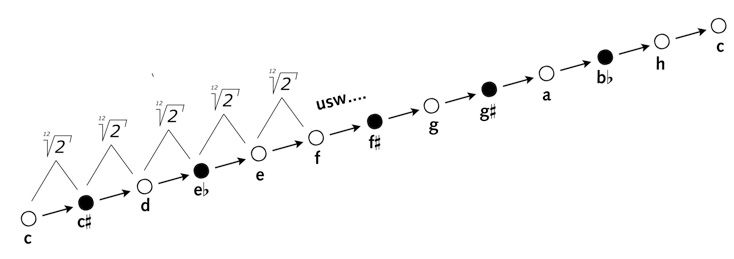
Oktave Wurzel 2
Bequem abmessen mit cent
In der Praxis müssen wir zum Glück nicht akribisch rechnen. Inzwischen gibt es ja digitale Stimmgeräte, und man kann sogar auf jedem Smartphone ein Stimmgerät als App installieren.
Eine Erleichterung, um Stimmungsfeinheiten zu messen:
Jeder Halbtonschritt wird (linear) in 100 Cent unterteilt.
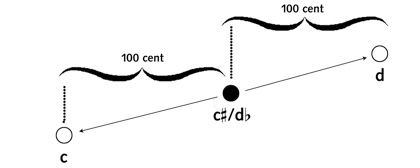
100 cent
Ein Ton, der um 20 cent zu hoch oder zu tief gestimmt ist, klingt schon deutlich falsch. Auf Stimmgeräten kannst du ablesen, um wie viel ein Ton von der gewünschten Stimmung abweicht.

stimmgerät
Stellt man alle Töne der Oktave in ihrem Verhältnis zum tiefsten Ton in cent dar, ergibt sich das dargestellte Bild:

1200 cent
Alles gleich? Alles Lüge!
Du siehst, wie genial in unserem Tonsystem alles ineinandergreift und zueinander passt. Um es noch einmal klarzustellen: Dass das geniale System funktioniert, fußt auf zwei Tatsachen:
erhöhte und erniedrigte Töne (z. B. cis und des) sind zu 100 Prozent gleich, haben also exakt die gleiche Frequenz.
Alle Halbtonschritte (d. h. jeder Schritt in der Tonkette c – cis – d – dis – e …) haben exakt dieselbe Größe, also dasselbe Frequenzverhältnis.
Die Ernüchterung: Beide Fakten sind gefälscht. Sie stimmen nicht – jedenfalls wenn man die natürlichen Schwingungsverhältnisse der Töne zugrunde legt. Warum und wie genau, das werden wir im Verlauf unserer Zeitreise entdecken.
Als junger Musiker empfand ich das als kleinen Schock. Natürlich hatte ich vom „pythagoräischen Komma“ und von der Einführung der „wohltemperierten“ oder „gleichschwebenden“ Stimmung gehört. Ich war aber überzeugt, das seien Kinderkrankheiten des Tonsystems im Mittelalter gewesen und seit Einführung der modernen Stimmung lägen alle früheren Stimmungen gewissermaßen auf dem Schrottplatz der Musikgeschichte. So hatte ich gedacht.
Mein Freund Andrej, der Konzertgeiger, klärte mich auf: Für jeden Geiger und jeden anderen Orchestermusiker ist es eine Selbstverständlichkeit, dass jedes fis höher intoniert wird (meist auch mit anderem Fingersatz) als ein ges. Was mich noch ein bisschen mehr schockierte: Geiger müssen, wenn sie mit Tasteninstrumenten zusammenspielen, sogar bewusst gröber intonieren, mit weniger Schärfe der Leittöne. Sie müssen die Feinheiten der Töne gewissermaßen ein bisschen plätten, damit es zusammen mit der „groben“ und unkorrekten Intonation des Klaviers klingt.
Genialer Betrug
Es ist also nicht zu leugnen: Hinter dem System, das uns auf dem Tasteninstrument die Freiheit zwischen allen Tonarten ermöglicht, steckt Betrug. Unsere moderne Stimmung beruht auf einer groß angelegten Fälschungsmaßnahme der Klavierbauer und Musiktheoretiker. Ohne dieses Fälschungsabenteuer wären wir in unwegsamen, verwirrend komplexen und (damals) ausweglosen Musiksystemen stecken geblieben.
In diesem und den folgenden Beiträgen möchte ich einige Stationen aufzeigen, die unsere Lehre von den Tönen genommen hat, bis die heutige Lösung erreicht war. Ich finde es faszinierend, wie viel Erfindergeist und wie viel geniale Suche in unser Musiksystem investiert wurde!
Ich werde versuchen, mit möglichst wenig Mathematik auszukommen (bin selbst kein Freund von Formelkram). Ein bisschen Rechnerei wird aber ab und zu nötig sein.
Aus akkordeon magazin #61, April/Mai 2018





0 Kommentare