In dieser Arbeit werden zwei Akkordeons beschrieben, bei denen mindestens ein Chor wohltemperiert und ein anderer gleichstufig gestimmt ist. Eine Jury beurteilte den Klang der wohltemperierten Stimmung in Tonarten mit wenigen Vorzeichen schöner als den der gleichstufigen und fand die Tonarten mit vielen Vorzeichen gleichwertig in beiden Temperierungen. Die wohltemperierten Stimmungen ermöglichen authentischere alte Musik als die gleichstufigen.
Die zwei verschieden gestimmten Chöre zusammen ergeben einen Tremolo-Klang. Bei dem einen Akkordeon, Weltmeister Stella 60, kommt die Temperierung der Werckmeister-III-Stimmung nahe. Bei dieser Stimmung ist das Tremolo sehr unregelmäßig. Um diesen Nachteil zu beheben, wurde eine zweite wohltemperierte Stimmung kreiert und mit einem Victoria Paganini Akkordeon verwirklicht. Diese Temperierung zeigt bessere Tremoli und erlaubt das Zusammenspiel mit anderen gleichstufigen Instrumenten. Weitere mathematische Optimierungen ergeben wohltemperierte Stimmungen mit einem schönen, sehr flachen Tremolo, welche aber aus finanziellen Gründen nicht verwirklicht und demnach auch nicht getestet werden konnten. Ferner wurde eine Möglichkeit gefunden, bei einem Knopfakkordeon mit einem sowohl auf der Bass- wie auch auf der Diskant-Seite modifizierten M2-Anordnung das Akkordeon so zu stimmen, dass in allen Tonarten die perfekte natürliche Stimmung verwirklicht werden kann.
Die Umstimmung eines Akkordeons auf wohltemperierte Stimmung ist etwa anderthalb bis zweimal aufwändiger als eine normale Akkordeonstimmung.
Text: Zoltán Faragó und Simone Wiech
Es gibt keine Stimmung, die an und für sich besser ist als eine andere, es gibt
nur bestimmte Stimmungen, die einen bestimmten Zweck besser erfüllen können
als andere. (Klaus Lang, 1999, p. 9)
Der Autor Zoltán Faragó (* 1942) ist Diplomingenieur. Nach sieben Jahren Forschung in der Industrie und sieben Jahren wissenschaftliche Tätigkeit in der Kernforschung arbeitete er vierzig Jahre lang in der Raumfahrtforschung. Einer seiner Arbeitsschwerpunkte war die Untersuchung der Einflüsse der Akustik von Raketenmotoren auf die Verbrennungsstabilität. Hier erwarb er Kenntnisse für akustische Messungen. Als Amateurmusiker hat er drei Jahrzehnte lang Orgel gespielt, unter anderem auf mehreren historischen Orgeln mit wohltemperierter und mit mitteltöniger Stimmung. Mit 77 Jahren fing er an Akkordeon zu spielen. Sein Wunsch ist, dass Barockmusik mit Akkordeon ähnlich schön klingt wie auf barocken Orgeln.
Die Autorin Simone Wiech (*1974) spielte schon in ihrer Kindheit verschiedene Musikinstrumente und interessierte sich gleichzeitig für handwerkliche Arbeiten an ihren Instrumenten. Als studierte Sozialpädagogin arbeitete sie mit autistischen Menschen und unterrichtete an einer Fachschule für Heilerziehungspflege, wo sie auch zum Leitungsteam gehörte. Nachdem sie 2011 ihre Leidenschaft für das Akkordeon entdeckt hatte, verwirklichte sie ab 2015 ihren Kindheitstraum, Musikinstrumente zu reparieren, und lernte in verschiedenen Werkstätten das Handwerk des Handzuginstrumentenbaus. Die Conzertina Werkstatt für Handzuginstrumente, gegründet am 1. Februar 2016, ist inzwischen bei Laien und Profis etabliert und entwickelt sich stetig weiter.
Disclaimer: Wenn das Geschlecht für einen bestimmten Zusammenhang ohne Bedeutung ist, verwenden die Autoren in einigen Fällen das generische Maskulinum in Plural für alle Geschlechter, um den Lesefluss nicht zu stören.
Gliederung:
Teil 1 Titel, Autoren, Kurzfassung, Motivation
Teil 2 Theoretischer Hintergrund
Teil 3 Die Praxis des Stimmens
2 Theoretischer Hintergrund
Ein Ton ist eine hörbare Schwingung, bei der Luftdruck und -geschwindigkeit periodisch abwechseln. Ein akustischer Klang besteht aus einer Vielzahl von Teiltönen, die als Sinuston dargestellt werden können. Der Grundton ist der tiefste Teilton, die höheren Teiltöne sind die Obertöne. Theoretisch beinhaltet ein Klang unendlich viele Teiltöne, messbar sind in der Regel 50 bis 100.
Der Klang wird durch Schwingung eines Körpers erzeugt. Die Schwingung kann aharmonisch oder harmonisch sein. Bei einer harmonischen Schwingung ist die Frequenz der Obertöne ein Produkt der Frequenz des Grundtons und einer natürlichen Zahl. Bei einer aharmonischen Schwingung gelten komplizierte mathematische Zusammenhänge zwischen Grundton und Obertönen (Z. Faragó et al, 2005). Aharmonische und harmonische Luftschwingungen werden als Klang wahrgenommen. Ein Klang besteht aus definierbaren, diskreten Frequenzen ihrer Teiltöne. Ein Geräusch beinhaltet alle hörbaren Frequenzen. Auch die harmonische Schwingung zeigt eine winzige Abweichung von der mathematisch exakten harmonischen Stimmung auf: Die Abweichung von der reinen Harmonie ist die Inharmonizität.

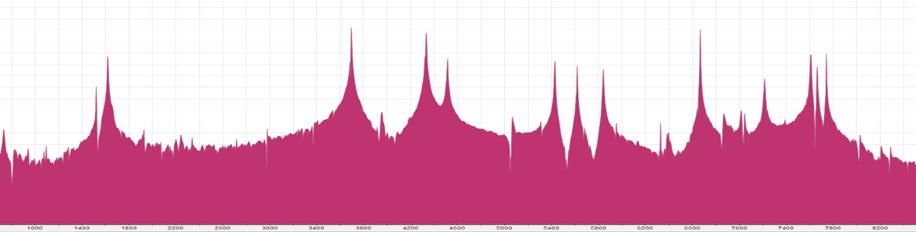
Abbildung 1
Grafische Darstellung eines Glockenklanges als Beispiel für einen aharmonischen Klang – gedämpfte Schwingung
Das obere Bild zeigt die Intensität der gedämpften Schwingung für zwei Sekunden. Die X-Achse ist die Zeit, die Y-Achse die Mikrofonspannung (Lautstärke). Im unteren Bild werden die Teiltöne des Glockenklanges dargestellt. Die X-Achse ist die Frequenz zwischen 900 und 8500 Hz, die Y-Achse ist die Intensität der einzelnen Sinustöne (ebenfalls Lautstärke). Im Bereich zwischen 10 und 22000 Hz können etwa 60 Sinustöne sicher nachgewiesen werden. Hierzu kommen circa 50 schwache und nicht ganz abgesicherte Signale mit wenig intensiven Teiltönen.
Die Aufnahme erfolgte mit einem t. bone USB-Mikrofon und dem Ocenaudio Audio Editor. Zur FFT-Analyse wurde die Blackman-Harris Fensterfunktion mit 65536 Blöcken ausgewählt.
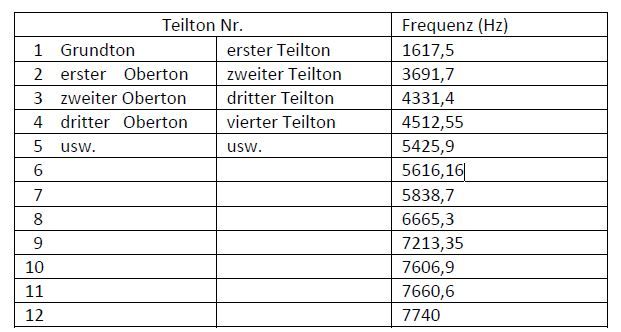
Tabelle 1
Frequenz der ersten 12 Teiltöne des in Abbildung 1 dargestellten aharmonischen Glockenklanges.
Bei den Teiltonbezeichnungen gilt: der n-te Teilton ist gleich mit dem (n-1)-ten Oberton. Der erste Teilton ist der Grundton.
Harmonische Schwingung
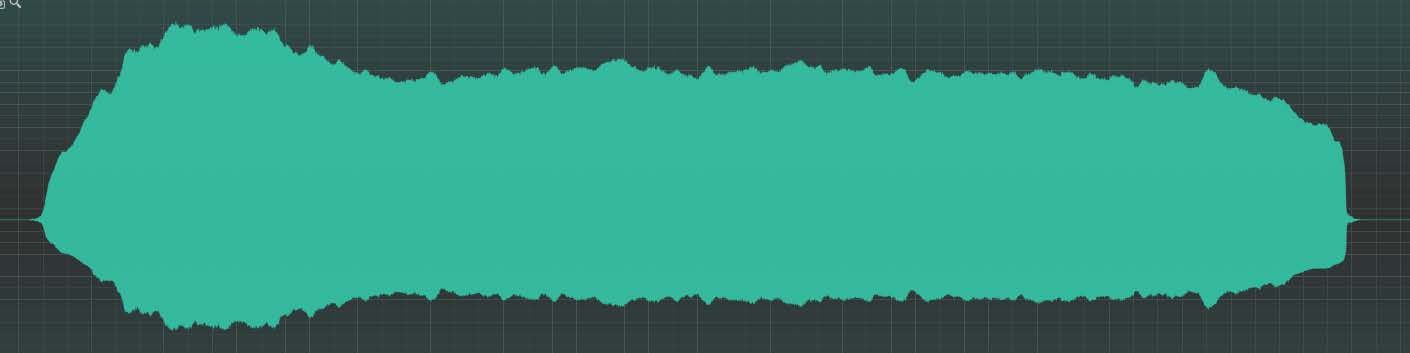
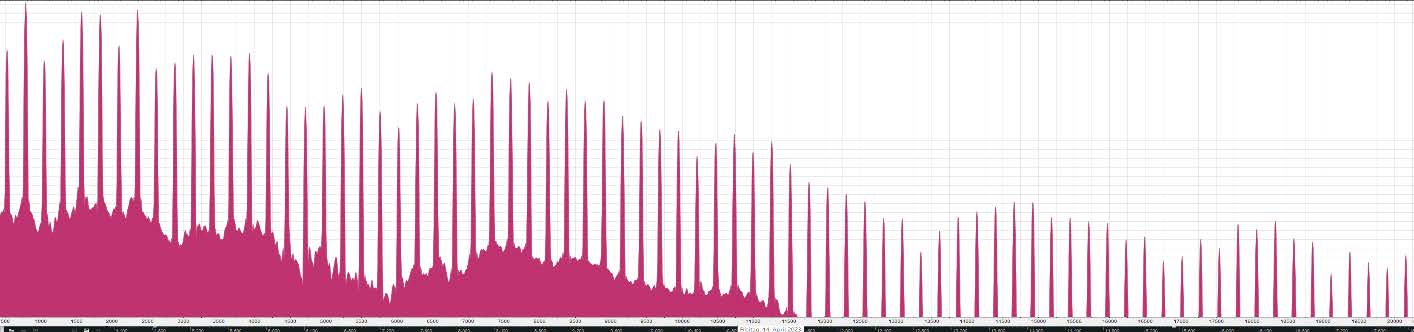
Abbildung 2
Grafische Darstellung des Akkordeonklanges (Stella 60) c‘ als Beispiel eines harmonischen Klanges – erzwungene Schwingung
Das obere Bild zeigt das Aufnahmesignal von 10,5 Sekunden Dauer, das untere die ersten 75 Teiltöne des Klanges. Die Aufnahmebedingungen sind identisch mit denen in Abbildung 1.
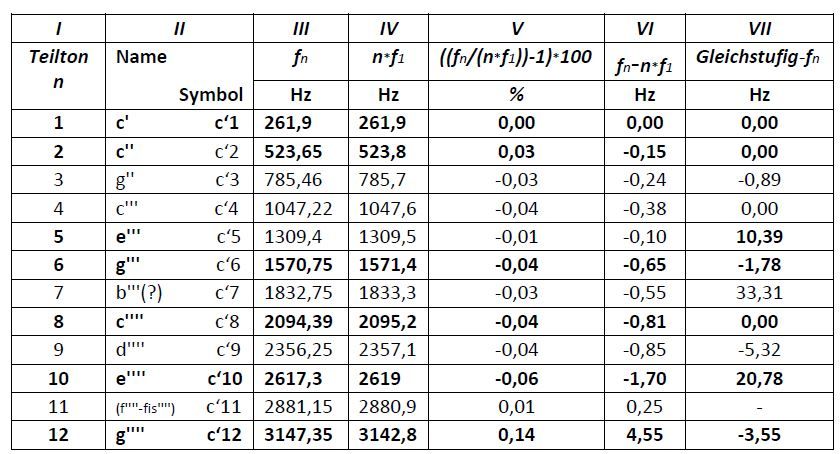
Tabelle 2
Analyse der ersten 12 Teiltöne des in Abbildung 2 dargestellten Akkordeonklanges
Die Spalte I in der Tabelle zeigt die Nummer, Spalte II die Namen der Teiltöne an. Die intensivsten Teiltöne sind die Nr. 2, 5, 6 und 8 (siehe Abbildung 2), sie sind für die Klangfarbe wichtig. Besonders wichtig für die Klangfarbe sind die Teiltöne Nr. 1, 2, 5, 6, 8, 10 und 12; sie bilden den Dur-Dreiklang des Grundtons. Sie sind in der Tabelle fett gedruckt. Spalte III zeigt die Teiltonfrequenzen fn des Tones c‘. In Spalte IV wird die Frequenz berechnet, die die jeweiligen Teiltöne ohne Inharmonizität hätten.
Die Inharmonizität, der Unterschied zwischen den Spalten III und IV, wird in Spalte V angezeigt. Sie liegt bis auf den 12. Teilton im hundertstel Prozentbereich. Die Inharmonizität beeinflusst die Klangfarbe und die Oktavreinheit.
Spalte VI zeigt die Schwebungsfrequenz an, die eine Inharmonizität verursacht. Die geringe Inharmonizitätsschwebung ist bis auf die 10. und 12. Teiltöne kaum hörbar.
Zum Vergleich zur Inharmonizitätsschwebung wird in Spalte VII die von der gleichstufigen Temperierung verursachte Schwebung aufgezeigt. Die Teiltöne des c–e Zweiklangs der gleichstufigen Temperierung (Teiltöne 5, und 10; e‘‘‘ und e‘‘‘‘) verursachen eine sehr starke Schwebung. Dies ist der Grund, warum sich diese Temperierung im 17. Jahrhundert nicht durchsetzen konnte. Das positive Vorzeichen bedeutet, dass die gleichschwebend temperierte Durterz im Vergleich zur natürlichen zu hoch ist (Oberschwebung). Der 7. Teilton ist die verminderte Septime. Hier ist die Schwebung besonders stark. Dies ist allerdings kein Nachteil, da die Dissonanz des dominanten Septakkordes in der Regel durch die nachfolgende Tonika aufgelöst wird. Der 11. Teilton ist auf einem zwölfstufigen Tasteninstrument nicht vorhanden. Beim Grundton c liegt dieser Teilton zwischen den Tönen f und fis.
Aus den Spalten VI und VII der Tabelle 2 wird sichtbar, dass die Oktavschwebung durch die Inharmonizität und die Terzschwebung durch die Temperierung verursacht wird.
Rauschen
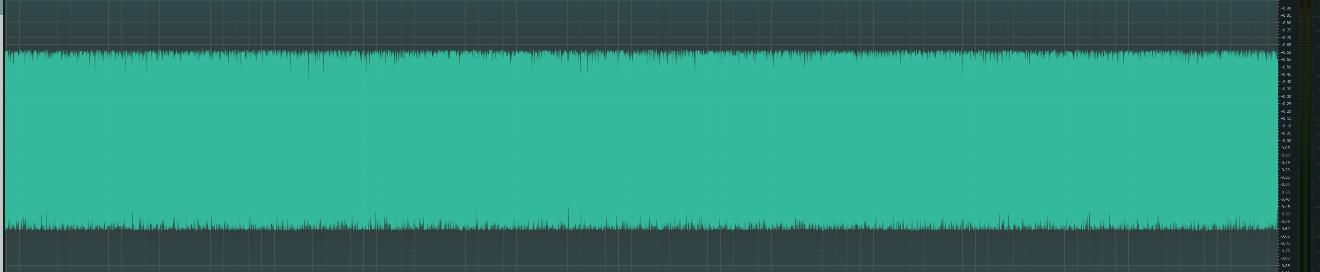

Abbildung 3
Grafische Darstellung des weißen Rauschens
Zur Illustration des Unterschiedes zwischen Rauschen und Klang werden in Abbildung 3 ein weißes Rauschsignal (oben) und seine Teiltöne (unten) dargestellt. Im oberen Bild ist die X-Achse die Zeit (Zeitdauer eine Sekunde), im unteren die Frequenz (100 bis 7000 Hz). Die Y-Achse ist in beiden Fällen die Mikrofonspannung. Der Unterschied zwischen Rauschen und Klang ist, dass das Rauschen jede Frequenz enthält und daher keine Tonhöhe hörbar ist.
Beim Hören eines Klanges ist immer ein kleines Rauschen wahrnehmbar. Dieses entsteht durch die Bewegung der Moleküle der Luft. Bei elektronischer Aufnahme und Wiedergabe kommt ein weiterer Rausch-Anteil hierzu. Dies ist bereits in den unteren Bildern in den ersten zwei Abbildungen sichtbar.
Schwebung zweier Töne
Die Schwebung ist eine periodische Änderung der Lautstärke des Klanges. Der obere Plot in Abbildung 2 zeigt eine durch die Inharmonizität verursachte Schwebung des einzelnen Tones c‘. Eine deutlich stärkere Schwebung entsteht, wenn gleichzeitig zwei Töne erklingen, die in der Tonhöhe eines Teiltones der beiden Töne nur um einen geringen Betrag voneinander entfernt sind. Ein Beispiel hierzu ist in Tabelle 4 und Abbildung 5 gezeigt
Beim Akkordeon erklingen immer wenigstens zwei Töne, auch, wenn man nur eine Taste oder einen Knopf betätigt. An jeder Stimmplatte sind zwei Zungen montiert. Immer wird eine davon durch Luftstrom angeregt (aktive Zunge), die andere (passive Zunge) wird durch die aktive Zunge in Schwingung gebracht. Die zwei Zungen schwingen annähernd gleich schnell, ein minimaler Unterschied tritt in der Tonhöhe immer auf, wie gezeigt in Tabelle 3. Alle Zungen gleicher Tonhöhe anderer Register werden ebenfalls mit angeregt. Auch die Obertöne der aktiven Zunge regen andere Zungen zur Schwingung an. Dadurch entsteht eine Vielzahl von Schwebungen, auch wenn nur eine einzige Taste betätigt wird.
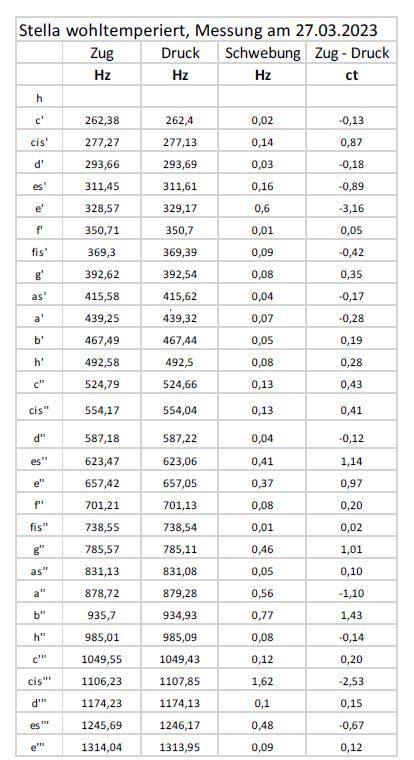
Tabelle 3
Frequenz (Hz) des 8‘ wohltemperierten Registers
Die Vielzahl der Schwebungen ist am besten an den im ANHANG B gezeigten Tabellen ersichtlich. In der Tabelle für die wohltemperierte Victoria Stimmung wird gezeigt, dass bei einem einzelnen Ton mitunter acht Zungen mit annähernd gleicher Frequenz schwingen. Zählt man die Oberton-Schwingungen auch dazu, erhöht sich die Anzahl der Schwebungen beträchtlich.
Erstellen von musikalischen Temperaturen
Es gibt einige Voraussetzungen, um eine musikalische Stimmung zu erstellen. Zuerst muss man die historischen Temperaturen kennen, die zu den darzustellenden Musikstücken passen. Ferner müssen die mathematisch-physikalischen Zusammenhänge der musikalischen Temperaturen bekannt sein. Schließlich muss die Technik zum Erstellen musikalischer Temperaturen beherrscht werden.
In der Zeit, in der die aus heutiger Sicht „alte Musik“ entstand, waren die Techniken zum Erstellen von Temperaturen anders als heute. Damals benutzte man Monochorde und geometrische Zeichnungen, um eine bestimmte Tonhöhe zu erreichen. Zu dieser Tonhöhe wurden die Töne schwebungsfrei gestimmt. Dabei führen verschiedene Stimmungstechniken zu verschiedenen Ergebnissen. Dieses kann am Beispiel der reinen Stimmung einer Gitarre gezeigt werden.
Methode 1
A Saite: 4. Teilton Flageolett mit Stimmgabel a‘ schwebungsfrei stimmen.
E Saite: 4. Teilton Flageolett und 3. Teilton von A Flageolett schwebungsfrei stimmen.
d Saite: 3. Teilton Flageolett mit 4. Teilton von A Flageolett schwebungsfrei stimmen.
g Saite: 3. Teilton Flageolett mit 2. Teilton von d Flageolett schwebungsfrei stimmen.
e‘ Saite: Grundton mit 4. Teilton von E Flageolett schwebungsfrei stimmen.
h Saite 4. Teilton Flageolett mit 6. Teilton von E Flageolett schwebungsfrei stimmen.
Diese natürliche Temperatur ist schöner als die gleichstufige, wenn man Gesang in a-, e– oder h– Dur begleitet, vorausgesetzt, kein gleichstufig gestimmtes Instrument spielt mit. Für Gesangsbegleitung in g– Dur ist diese Stimmung nicht geeignet.
Methode 2
Die Stimmung der Saiten A, E, d, g und e‘ ist identisch mit Methode 1.
h Saite: 2. Teilton Flageolett mit 3. Teilton von g Flageolett schwebungsfrei stimmen.
Diese ebenfalls natürliche Temperatur ist schöner als die gleichstufige in g– und d– Dur.
Weitere Methoden zu beschreiben und auszuführen ist viel schwieriger. Eine Gitarre nach Gehör gleichstufig zu stimmen, benötigt viel Erfahrung. Das Stimmen mit Stimmgerät ist eine Erleichterung.
Will man in mehr als drei Tonarten mit einer Temperatur spielen, muss man den einen oder anderen Ton der Tonleiter mit gewisser Schwebung beim Zweiklang mit der Prime einstellen. Je mehr Tonarten in einer Komposition enthalten sind, umso mehr Kompromisse sind in der Erstellung der musikalischen Temperatur nötig.
In verschiedenen Stimmungsanweisungen wurde im Mittelalter und später beschrieben, welche Töne mit welchen anderen Tönen schwebungsfrei zu stimmen sind und welche um welchen Betrag Schwebungen erhalten. Diese Beschreibungen sind nicht immer eindeutig. Für die eine oder andere historische Stimmung gibt es mehrere Interpretationen.
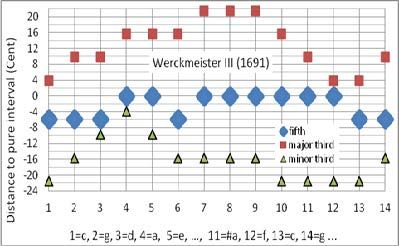
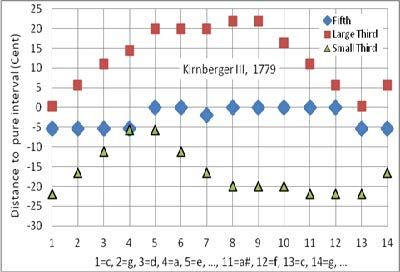
Abbildung 4
Grafische Darstellung zwei wohltemperierter Stimmungen
Quelle: http://www.farago.info/hobby/musikAkustik.html
Die in Abbildung 4 dargestellten Temperaturen gehören zu den bekanntesten in der Barockmusik. Die X-Achse stellt die Tonarten nach dem Quintenzirkel dar. Die Y-Achse zeigt an, um welchen Cent-Betrag die Dur- und Mollterz beziehungsweise die Quint von der natürlichen Stimmung abweichen. Bei Y=0 ist der entsprechende Zweiklang schwebungsfrei. Bei positiven Y-Werten tritt ein Tremolo als Oberschwebung, bei negativen Werten als Unterschwebung auf.
Bei der Werckmeister-III-Stimmung sieht man, dass die Quinten für die Töne c, g, d und h um ¼ des pythagoreischen Kommas verengt wurden. Das pythagoreische Komma (PK) ist der Unterschied zwischen 12 reinen Quinten und 7 reinen Oktaven, PK = 23,460002 ct. Das syntonische Komma (SK) ist der Unterschied zwischen dem großen und dem kleinen Ganzton, SK = 21,506 ct. Das Schisma (Sch) ist der Unterschied zwischen dem PK und dem SK, Sch = 1,954002 ct. Ein zwölftel des PK ist der Werckmeister (WM), WM = 1,955000167 ct. WM minus Sch beträgt lediglich 0,0009982 ct.
Die Schärfe der Durterz nimmt in der Werckmeister-III-Stimmung von C-Dur bis Fis-Dur in drei gleichgroßen Stufen zu, von As-Dur bis F-Dur in gleichgroßen Stufen wieder ab.
Bei der Kirnberger-III-Stimmung werden die Quinten zwischen c und a um ¼ des syntonischen Kommas verengt. Die Quinten der anderen Töne bis auf fis sind rein, die Quint von fis verkleinert sich automatisch um das Schisma. Die Stimmungsanweisung lautet: Die c-e Terz wird schwebungsfrei gestimmt. Die c-g, g-d und d-a Quinten werden um einen kleinen Betrag verengt. Die so entstandene a-e Quint wird verglichen mit den c-g, g-d und d-a Quinten. Dieser Vorgang wird so lange wiederholt, bis die vier Quinten etwa gleich klingen. Die Quinten zu e und h werden schwebungsfrei gestimmt. Die Unterquinten zu c, f, b, es, as und des werden auch schwebungsfrei gestimmt. Die verbliebene Quint fis-cis verkleinert sich automatisch um das Schisma.
Das Diagramm der Kirnberger-III-Stimmung in Abbildung 4 stellt die Dur- und Moll-Terzen und Dur-Dreiklänge dar, wenn die Stimmung mathematisch korrekt, das heißt, absolut fehlerfrei ist. Das ist praktisch nie der Fall. Wie groß der Unterschied zwischen der mathematischen Berechnung und der praktischen Durchführung einer Stimmung sein kann, wird in den Abbildungen 9 und 10 sichtbar.
Akkordeonspezifische Phänomene
Der Klang des Akkordeons hat starke Obertöne. In Abbildung 2 sieht man beispielhaft, dass bei dem Ton c‘ von den ersten sieben Obertönen sechs lauter sind als der Grundton selbst. Bei tieferen Tönen sind oft mehr als zehn Obertöne lauter als der Grundton. Die ersten fünf Obertöne ergeben den Dur-Dreiklang des Grundtones, unter den ersten zwölf Obertönen sind zehn Bestandteil der natürlichen Dur-Tonleiter (siehe Tabelle 2). Bei starken Obertönen entsteht eine laute, stark hörbare Schwebung, wenn bei gleichzeitigen erklingen zweier Töne einiger ihrer Teiltöne geringfügig voneinander abweichen. Bei gleichstufig gestimmtem Akkordeon ist das immer der Fall. Bei wohltemperierter Stimmung ist dies bei Tonarten mit wenigen Vorzeichen schwächer ausgeprägt. Daher ist eine ungleichmäßige Temperierung vorteilhaft, wenn man die Schönheit der historischen Temperierung für Alte Musik beim Akkordeon erhalten will.
Das obere Bild in Abbildung 5 zeigt das Aufnahmesignal der Töne c‘ und e‘ und der Zweiklänge c‘-e‘.
Der Zeitdauer der Einzeltöne ist 1,5 Sekunde, bei den Zweiklängen 2,5. Die Einzeltöne und der erste Zweiklang sind gleichstufig, der zweite Zweiklang ist wohltemperiert.
Das mittlere Bild zeigt die Frequenzen der Grund- und Obertöne des gleichstufigen c‘-e‘-Zweiklanges im Bereich von 200 bis 2000 Herz, während das untere Bild die Teiltöne des wohltemperierten Zwei-klanges darstellt. Die Cursorposition und der dicke Doppelpfeil liegen bei 1310 Hz. Der fünfte Ober-ton von c‘ (gleichstufig) hat die Frequenz 1306,31 Hz, der vierte Oberton von e‘ (gleichstufig) 1317,025 Hz. Diese zwei getrennten Töne sind erkennbar im mittleren Bild, während sie im unteren Bild zu einem Ton verschmelzen. Die dünnen Doppelpfeile zeigen weitere Bereiche an, wo mehrere virtuelle Töne der gleichstufigen Stimmung bei der wohltemperierten Version zu jeweils einem Ton zusammenschmelzen. Dieser Effekt ist hörbar: Der wohltemperierte Zweiklang ist weicher als der gleichstufige, es enthält weniger virtuelle Teiltöne und weniger Schwebungen, wie gezeigt in Abbildung 5.
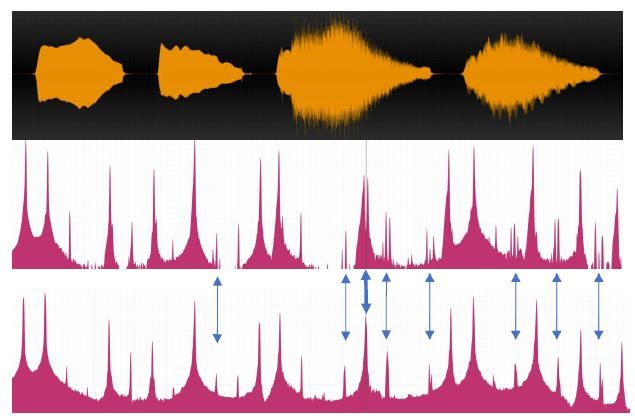
Abbildung 5
Audioplot der Töne c‘, e‘ und der Zweiklänge c‘-e‘. Oberes Bild: Soloklänge c‘ und e‘ (Zeitdauer ca. 1,5 s), c‘-e‘ Zweiklänge (ca. 2,5 s) gleichstufig und wohltemperiert. Mittleres Bild: Teiltonbilder des gleichstufigen c‘-e‘ Zweiklanges. Unteres Bild: Teiltonbilder des wohltemperierten c‘-e‘ Zweiklanges.
Die ersten sieben starken Piecks sind die Teiltöne (Hz, unteres Bild): c‘ 262,31; e‘ 329,11; c‘2 524,78; e‘2 658,17; c‘3 787,23; e‘3 987,21; c‘4 1049,55. Die Teiltöne c‘5 und e‘4 haben annähernd die gleiche Frequenz (1313,8 Hz, siehe dicken Doppelpfeil). Die kleineren Piecks sind Residualtöne (virtuelle Teiltöne). In Abbildung 5 wird optisch sichtbar gemacht, dass der wohltemperierte c-e-Zweiklang deutlich weicher ist als der gleichstufige.

Tabelle 4
Frequenzen einiger in Abbildung 5 gezeigten Töne und Obertöne
In Tabelle 4 bedeuten: c‘ und e‘ (unterstrichen) sind Grundtöne, c‘5 und e‘4 die zugehörigen Teiltöne (für die Nomenklatur siehe Tabelle 2). Bei c‘-e‘ erklingen zwei Töne, die Frequenz des unterstrichenen Teiltons wird angegeben. Für den C-Dur-Dreiklang c‘-e‘-g‘ ist ebenfalls die Frequenz des unterstrichenen Teiltons angegeben. Die nicht-unterstrichene Töne klingen mit, ihre Frequenzen wurden nicht gemessen. gl.st =gleichstufig, w.t.=wohltemperiert.
Beim Vergleich des mittleren und des unteren Bildes in Abbildung 5 muss berücksichtigt werden, dass es sich hier um zwei verschiedene Akkordeons handelt (siehe Abbildung 8). Das gleichstufig gestimmte Instrument ist ein Melodiebass Victoria Paganini mit 37 Pianotasten und drei Diskantchören (16‘, 8‘, 4‘). Das wohltemperierte Akkordeon ist hingegen ein Victoria Paganini mit 34 Pianotasten und zwei Diskantchören (8‘, 4‘). Bassseitig sind die zwei Instrumente identisch.
Neben den starken Obertönen gibt es einige akkordeonspezifische Klangeigenschaften, die die Umstellung der gleichstufigen auf die wohltemperierte Temperatur erschweren. Die wichtigsten davon sind die Tonhöhenabhängigkeit von der Lautstärke (Abbildung 6) und von der Zeitdauer (Abbildung 7) des gespielten Tones.
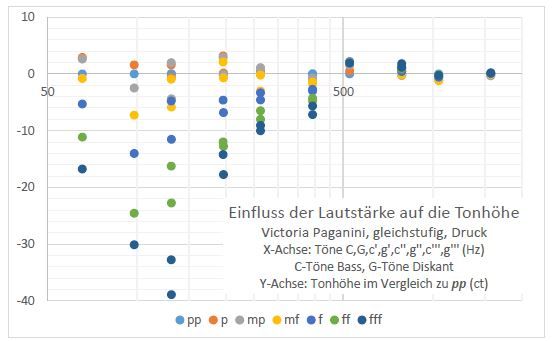
Abbildung 6
Einfluss der Lautstärke auf die Tonhöhe
Alle c- und g-Töne von C (~65 Hz) bis g‘‘‘ (~1573 Hz) wurden vermessen. Die Tonlänge war jeweils etwa 10 Sekunden, angefangen mit Pianissimo und kontinuierlich verstärkt bis Fortisissimo. Die Tonfrequenz wurde in sieben Lautstärkenstufen analysiert. Die Differenz in Cent zu Pianissimo ist in Abbildung 6 als Messwert eingetragen. Aus dem Diagramm ist erkennbar, dass bei pp bis mp die Tonhöhe unabhängig ist von der Lautstärke. Von mf bis fff nimmt die Abhängigkeit der Tonhöhe von der Lautstärke ständig zu. Dieser Effekt ist bei den tiefen Tönen besonders stark.
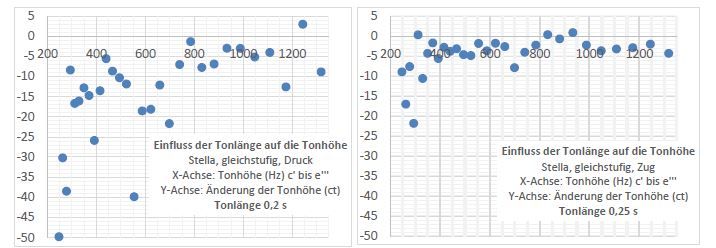
Abbildung 7
Einfluss der Tonlänge auf die Tonhöhe
In Diagramm 7 ist der Einfluss der Tonlänge auf die Tonhöhe gezeigt. Jeder Ton zwischen c‘ (~ 262 Hz) und e‘‘‘ (~1314 Hz) wurde zweimal ausgewertet. Der Ton war Sekunden lang. Im linken Bild ist die Tonhöhe in den ersten 0,2 Sekunden ausgewertet und mit der Tonhöhe nach der Einschwingzeit verglichen. Im rechten Bild sind die ersten 0,25 Sekunden ausgewertet. In den Plots wurde die Differenz der beiden Tonhöhen in Cent eingetragen. Die X-Achse zeigt die Frequenz an, die Y-Achse die Differenz der Tonhöhe zwischen Tonanfang und Tonende. Demnach beträgt die Einschwingzeit der tiefen Töne 0,3 bis 0,4 Sekunden.
Die zeitliche Entwicklung der Tonhöhe von C (65 Hz) und g (196 Hz) wird in Abbildung 11 graphisch dargestellt.
Zusammenfassung der akkordeonspezifischen Phänomene:
Alle Töne des Akkordeons sind durch die Druckschwingung im Balg miteinander verbunden und beeinflussen sich gegenseitig. Die Frequenz eines Tones ändert sich, wenn ein anderer Ton mit einem verwandten Obertonspektrum angespielt wird. Dieser Effekt kann mehrere Cent betragen.
Die Tonhöhe wird im Frequenzbereich unterhalb 500 Hz von der Lautstärke beeinflusst. In der eingestrichenen Oktave kann die Tonhöhe bei fortissimo im Vergleich zu pianissimo bis um 10 Cent absinken. Bei tieferen Oktaven verstärkt sich dieser Effekt bis auf 40 Cent. In der Einschwingphase erklingen die Töne tiefer. Unterhalb 500 Hz können die Töne bei Stakkato und Bellowshake um bis zu 50 Cent tiefer klingen als nach der Einschwingzeit. Eine Verkürzung der Einschwingzeit kann durch konstruktive Änderung an den Stimmplatten erreicht werden. Ein weiterentwickeltes Stimmgerät, das nicht nur die endgültige Tonhöhe, sondern auch Zwischenwerte nach ¼, ½, ¾ und 1 Sekunde „einfriert“ und anzeigt, würde nicht nur das Stimmen, sondern auch die Entwicklung von diesbezüglich optimierten Stimmplatten erleichtern.
Die Vorgehensweise des Projektes
Um die anfangs gestellte Frage, ob durch eine kleine Abweichung von der gleichstufigen Stimmung der Klang eines Akkordeons verbessert werden kann, zu beantworten, wurden in der Werkstatt für Handzuginstrumente, Conzertina Nürnberg, zwei Akkordeons auf wohltemperierte Stimmungen umgestimmt. Das Ziel war, die Stimmungen so zu gestalten, dass die wohltemperierten Akkordeons mit gleichstufig gestimmten Instrumenten zusammenspielen können. Ferner mussten die Autoren akkordeonspezifische Phänomene berücksichtigen.
Eines des beiden Akkordeons war ein Weltmeister Stella 60, bei dem das 8‘-Tremolo-Chor auf wohltemperiert umgestimmt wurde, während der andere 8‘-Chor gleichstufig geblieben ist. Das zweite Akkordeon war ein Victoria Paganini. Es hat nur einen 8‘-Chor, der umgestimmt wurde. Um einen Vergleich zwischen wohltemperiert und gleichstufig zu ermöglichen, behielt ein zweites Victoria Paganini die gleichstufige Temperierung.
Die einzelnen Stufen sind:
1) Erstellen einer Temperatur für die Musik des 18. Jahrhunderts mit Anlehnung an die Werckmeister Stimmung. Um das Ziel, einen wohltemperierten Chor mit einem gleichstufig temperierten zusammen spielen zu können, weicht die so entstandene Stimmung von der Werckmeister Stimmung geringfügig ab, wie gezeigt in den Diagrammen 4 und 9. Die neue Stimmung wird hier als Stella Temperatur bezeichnet.
2) Umstimmung eines Stella 60 Akkordeons auf die Stella Temperatur, so dass der 8‘-Chor gleichstufig bleibt, das Tremolo und der 16‘-Chor auf wohltemperiert umgestellt werden, und die Bass-Seite eine 50-prozentige Mischung der beiden Temperaturen erhält.
3) Ausprobieren der wohltemperierten Stimmung: Zuerst wurden 8‘-gleichstufig mit 8‘-wohltemperiert, dann 8‘-gleichstufig mit 16‘-wohltemperiert, danach die Tremolo-Schaltung, d.h. gleichstufig und wohltemperiert zusammen angehört. Dabei hat sich gezeigt, dass die Tremolo Schaltung der neuen Temperatur viel zu unruhig und bei einigen Tönen zu scharf ist. Auf diesen Erkenntnissen basierend wurde eine neue Temperatur berechnet.
4) Die so entwickelte neue Temperatur wurde mit einem Victoria Paganini verwirklicht. Diese wird in vorliegender Arbeit als Victoria Temperatur bezeichnet (Diagramm 10). Da die Victoria Paganini Akkordeons nur einen 8‘-Chor haben, wurde ein Akkordeon auf die Victoria Temperatur umgestellt, das andere wurde gleichstufig gelassen. Das Ausprobieren der Victoria Temperatur erfolgte auf ähnliche Weise wie beim Stella 60 Akkordeon, mit dem Unterschied, dass bei der Tremolo Schaltung hier beide Akkordeons gleichzeitig gespielt wurden. Das Ergebnis war ein viel schöneres, aber immer noch nicht perfektes Tremolo.
5) Auf dieser Erkenntnis basierend wurden weitere neue Stimmungen berechnet, um beim Zusammenklang wohltemperierter und gleichstufiger Chöre ein optimales Tremolo zu erreichen. Dies soll neue, auf dem Akkordeon bisher nicht bekannte Klangfarben ermöglichen. Die Verwirklichung einer solchen Temperatur übersteigt die finanziellen Möglichkeiten der Autoren. Diese Arbeit kann nur fortgeführt werden, wenn eine Institution, Stiftung oder ein Akkordeonhersteller die begonnene Forschung finanziell unterstützt.





0 Kommentare