Der lange Weg zu unserem Musiksystem (Folge 1)
Der lange Weg zu unserem Musiksystem (Folge 2)
Die moderne, „gleichschwebende“ Stimmung unserer Tasteninstrumente beruht genau genommen auf gefälschten Tatsachen und verfälschten Intervallen. Orchestermusiker aller Instrumente spielen keineswegs temperiert; mitunter müssen sie ihre Tonbildung sogar vergröbernd anpassen, wenn sie mit Tasteninstrumenten zusammen spielen. Das war die etwas irritierende Tatsache, auf die wir am Ende der ersten Folge dieser Kolumne gestoßen sind.
Text: Peter M. Haas
Naturklänge? Oberschwingungen!
Wenn behauptet wird, die temperierten Intervalle der Klaviere, Orgeln und Akkordeons seien falsch – woran misst sich das überhaupt? Woran soll man denn die angeblich richtigen Intervalle erkennen?
Den Grundstein hat schon Meistermathematiker Pythagoras vor über 2000 Jahren gelegt. Auf seine Experimente geht im Grunde alles zurück, was wir über Tonverwandtschaften wissen.
Pythagoras experimentierte mit einer schwingenden Saite, dem sogenannten Monochord, und fand heraus:
schwi-1
Für diese und die folgenden Schwingungsgrafiken habe ich eine Grafik von Y. Landman/wiki verwendet – danke! https://commons.wikimedia.org/wiki/File:Moodswingerscale.svg
Oktave
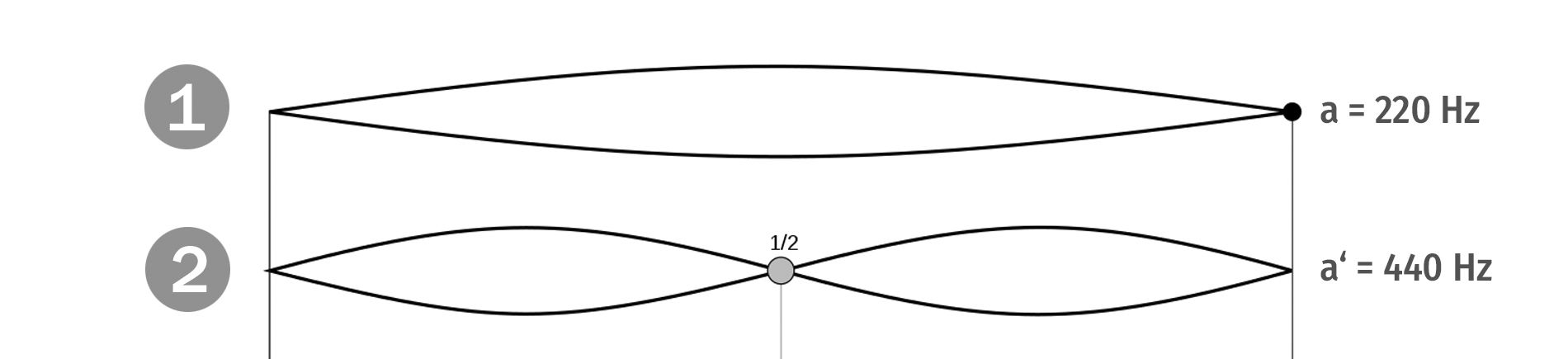
Wenn ich eine Saite auf die halbe Länge verkürze, schwingt sie doppelt so schnell. (Wir sagen heute: Sie hat die doppelte Frequenz.) Es erklingt ein Ton, der eine Oktave höher ist. Ein Beispiel: Wenn mein Ausgangston das a ist („kleines a“ mit der Frequenz 220 Hz), dann ist mein zweiter Ton also a‘ („eingestrichenes a“ mit der Frequenz 440 Hz). Grundsätzlich kann ich folgern: Das Schwingungsverhältnis jeder beliebigen Oktave ist 1 : 2.
schwi-2
Quinte
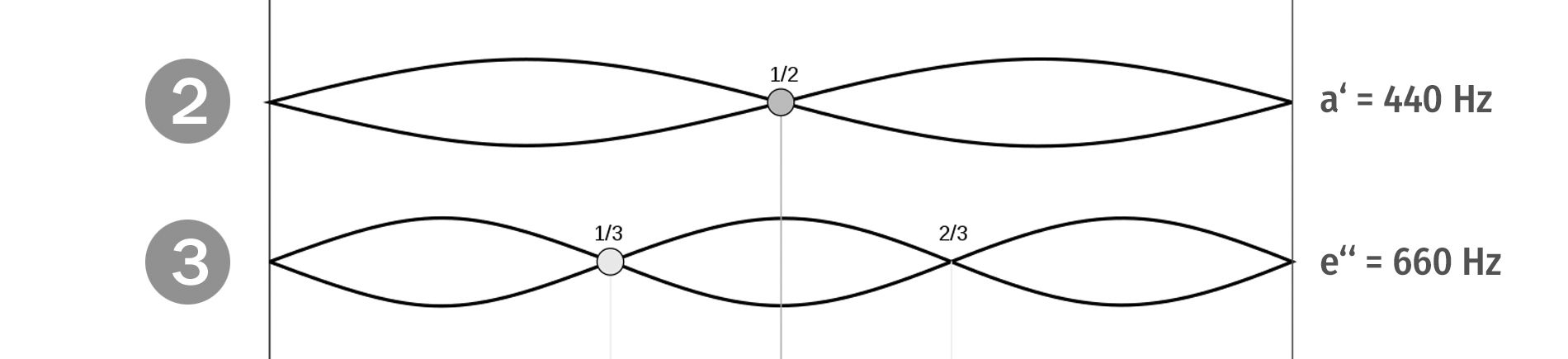
Wenn ich meine ursprüngliche Saite auf ein Drittel verkürze, schwingt sie dreimal so schnell, und es erklingt ein Ton, der eine Quinte höher ist als mein Ton Nummer 2. In unserem konkreten Fall also das e“ („zweigestrichenes e“ mit der Frequenz 660 Hz). Grundsätzlich kann ich folgern: Das Schwingungsverhältnis jeder beliebigen Quinte ist 2 : 3.
schwi-3
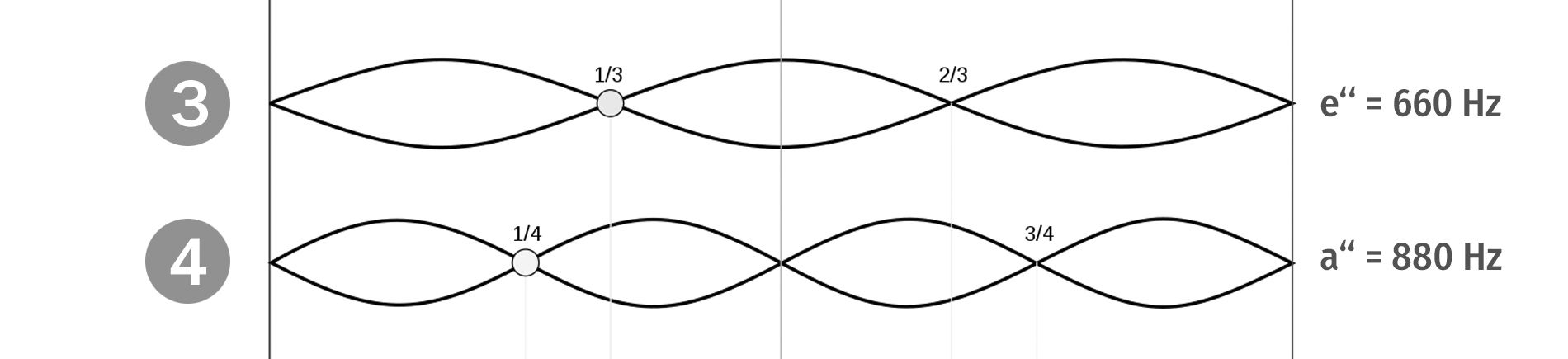
Weiter als bis vier hat Pythagoras nicht gezählt. Vielleicht konnte er nicht, weil damals die Gegebenheiten für genauere Messungen von Achtel-, Zehntel- und Zwölftelsaiten nicht gegeben waren. Vielleicht wollte er aber auch gar nicht.
Teiltöne Grafik
Aus den Intervallen Oktave, Quarte und Quinte leitete er sein System zur Berechnung der Töne ab; mehr Intervalle hätten ziemlich sicher das stabile Gefüge ins Wanken gebracht. (Ohnehin lag dem Meister viel daran zu beweisen, dass dem ganzen Weltgefüge und dessen Harmonie die Verhältnisse einfachster, gerader Zahlen zugrunde liegen, und es ist überliefert, dass er manche Tatsachen, die diese Harmonie stören konnten, sehr wohl kannte, aber nicht öffentlich machte.)
Über die gesamte Dauer des europäischen Mittelalters blieb es dabei, dass nur diese drei Intervalle – Oktave, Quarte und Quinte – als Konsonanzen galten. Entsprechend klang auch die Musik dieser Zeit. Erst die Renaissance „erfand“ Dur- und Molldreiklang und damit die große und die kleine Terz als konsonante Intervalle.
Höher hinaus
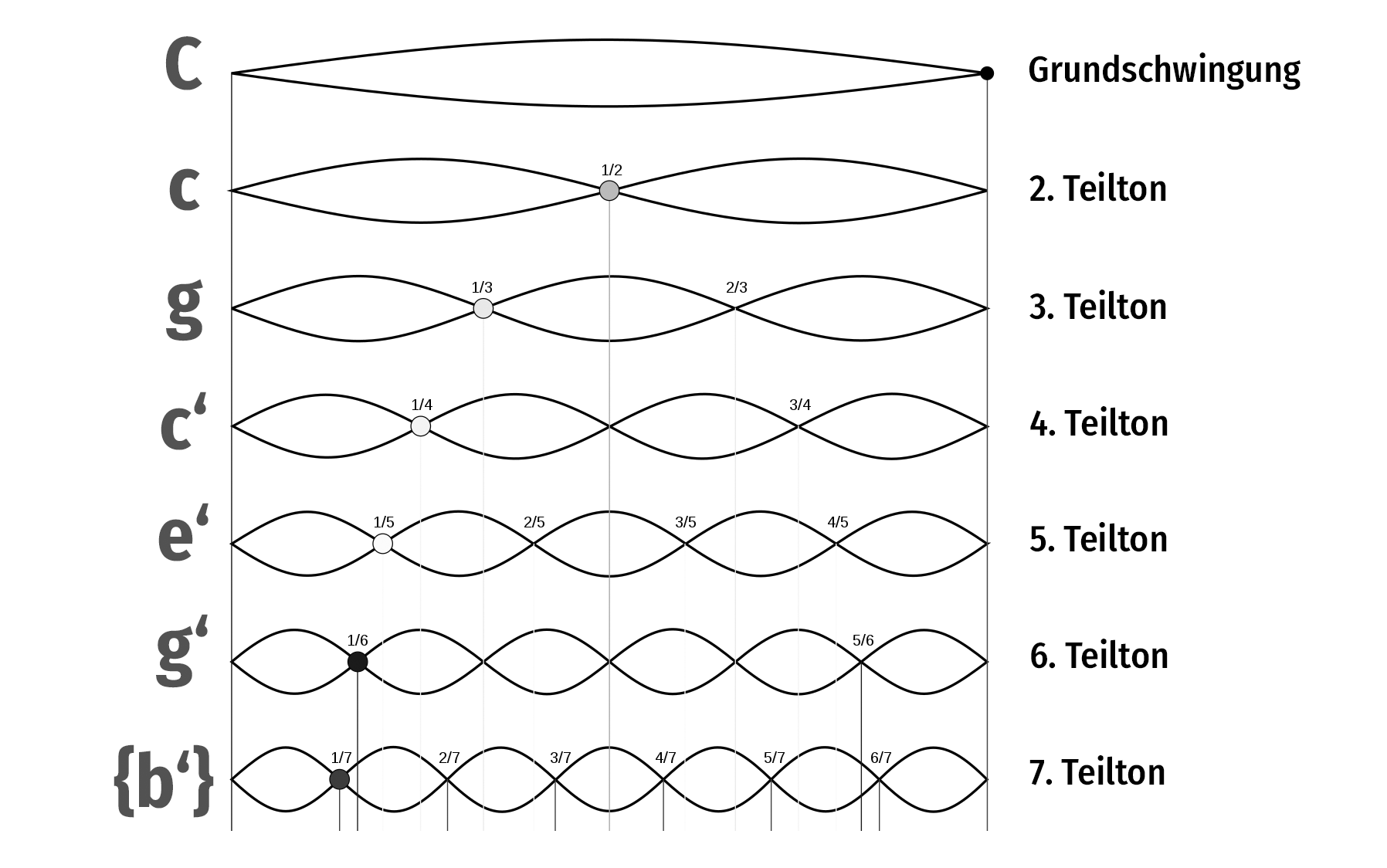
Aber natürlich kann man die Folge der Schwingungen, die entstehen, weiterführen, indem die Saite auf ein Fünftel, ein Sechstel usw. verkürzt wird. Es sind dann allerdings die Mittel der neuzeitlichen Physik nötig, um die Frequenzen einzelner Töne genau zu messen: Von grundlegender Bedeutung waren hierfür die Forschungsergebnisse des Franzosen Joseph Saveur (1653 – 1716) und des deutschen Physikers Hermann von Helmholtz (1821 – 1894). Jetzt wissen wir, dass jeder gespielte Ton seine Oberschwingungen (also die Töne mit zweifacher, dreifacher, vierfacher usw. Frequenz) als Teiltöne beinhaltet. Die folgende Grafik zeigt die Schwingungen des ersten bis siebten Teiltones und die resultierenden Teiltöne des Grundtones C (großes C).
Es macht Sinn, die Teiltöne noch über den 8. Teilton hinaus zu berücksichtigen. Hier sieht man als Beispiel die Folge der Teiltöne über dem Ton C („großes C“) bis zum 16. Teilton:
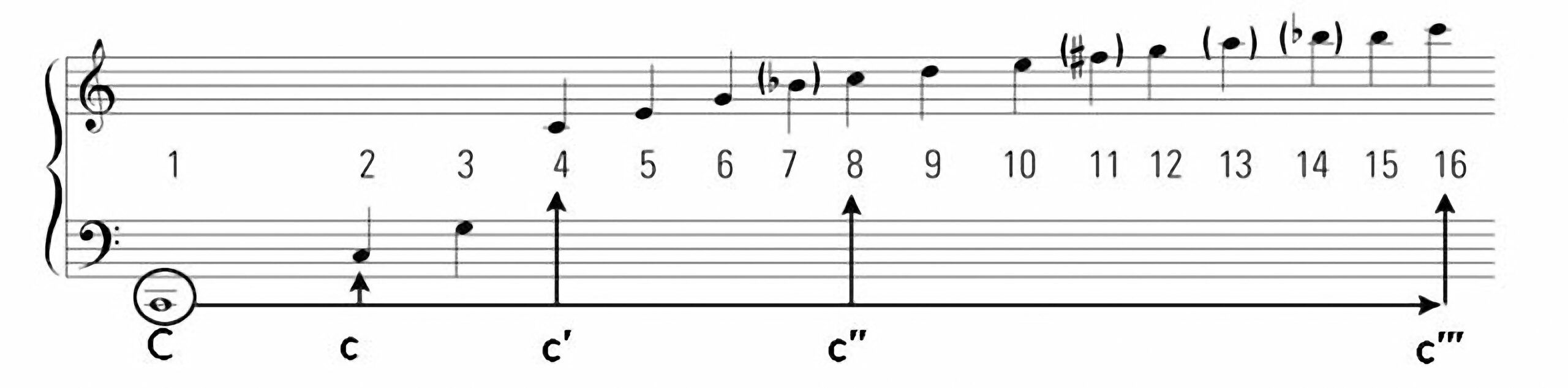
NOTE-OBERTÖNE_uspcled
So wie wir es mit Pythagoras für die ersten vier Teiltöne gemacht haben, kann man leicht das Schwingungsverhältnis jedes beliebigen Intervalls aus der Rangfolge jedes Teiltones ablesen. Nehmen wir als Beispiel die große Terz – Wir finden sie im Verhältnis von c‘ (4. Teilton) zu e‘ (5. Teilton). Große Terz = c‘ (4-fache Grundfrequenz) zu e‘ (5-fache Grundfrequenz) = 4 : 5. Oder die große Sekunde – Wir finden sie im Verhältnis von c“ (8. Teilton) zu d“ (9. Teilton). Große Sekunde = c“ (8-fache Grundfrequenz) zu d“ (9-fache Grundfrequenz) = 8 : 9.
sphären
Einige Töne im Notenbeispiel sind in Klammern gesetzt – der 7., 11., 13. und 14. Teilton haben Frequenzen, die nicht sauber in unser Tonsystem und unsere Hörerwartung passen.
Teilton – Oberton
Manchmal spricht man auch von Obertönen. In jedem Ton, der auf einem Instrument gespielt wird, erklingt nicht nur die Grundfrequenz (sonst würde man einen sehr dumpfen, matten Ton hören), sondern auch – in unterschiedlichen Anteilen – die Teiltöne als Obertöne. Was man Obertöne nennt, sind exakt die Teiltöne, die wir eben im Notenbild gezeigt haben, nur die Nummerierung ist abweichend: Der Grundton selbst wird nicht mitgezählt. Als erster Oberton erklingt also der zweite Teilton, und entsprechend verschiebt sich die Nummerierung für alle folgenden Obertöne.
Wichtig ist das zum Beispiel für die Klangmixtur in Orgeln, deutlich sichtbar auch bei der Hammond-Orgel: Durch Zugriegel kann man dort dem weich schwingenden Grundton Obertöne hinzufügen und den Klang dadurch heller und schärfer machen. Hat vielleicht jemand unter euch das Musikprogramm Logic oder Cubase? Da ist eine wunderbare Vintage B3-Hammondorgel als virtuelles Instrument integriert.
Naturklang contra temperierte Stimmung
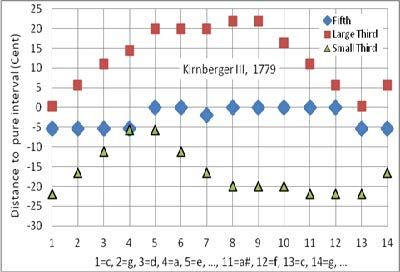
Die Stimmung unserer Töne sollte also wohl diesen Naturklangsverwandtschaften folgen, um größtmögliche Harmonie zu erzeugen, nicht wahr? Das tut sie aber nicht, wie ein Vergleich der natürlichen Schwingungsverhältnisse mit den Frequenzen der temperierten Stimmung zeigt. (Ehrlich gesagt habe ich das nicht selbst nachgerechnet, sondern direk taus dem Lexikon übernommen.): Alle „natürlichen“ Intervalle weichen von dem gleichschwebenden Raster der temperierten Stimmung ab; manche nur um wenige cent, andere – wie die große Terz – bis zu 14 cent, was bereits eine sehr deutlich hörbare Verstimmung ist.
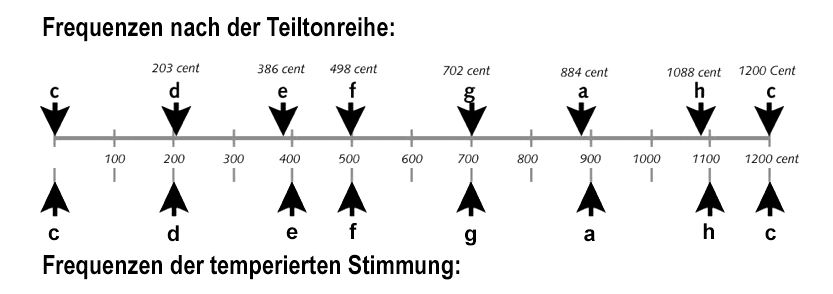
Frequenzen
Nichts passt in der Natur
Warum gibt es diese Abweichung? Warum hat man nicht einfach die Schwingungsverhältnisse der Obertonreihe zur Stimmung unserer Tastatur übernommen?
Die Antwort ist ganz einfach – aus diesen natürlichen Schwingungsverhältnissen lässt sich kein funktionierendes Tonsystem bauen. Sobald man den einen, einzigen Grundton verlässt und andere Tonleitern bilden will, ergibt sich ein Widerspruch und Rechenfehler nach dem anderen, umso mehr, je weiter man sich vorwagt.
Ein einziges, etwas verblüffendes Beispiel: Die Folge der Teiltöne enthält rechnerisch und faktisch zwei verschieden bemessene Ganztonschritte!
Wir finden die große Sekunde, wie oben schon erklärt, im Verhältnis von c“ (8. Teilton) zu d“ (9. Teilton). Große Sekunde = c“ (8-fache Grundfrequenz) zu d“ (9-fache Grundfrequenz) = 8 : 9. Eine anders bemessene große Sekunde finden wir aber im Verhältnis von d“ (9. Teilton) zu e“ (10. Teilton). Große Sekunde = d“– (9-fache Grundfrequenz) zu e“ (10-fache Grundfrequenz) = 9 : 10.
Wollte ich also jetzt mit dem vorhandenen Tonmaterial die D-Dur-Tonleiter wohlklingend spielen – als Abbild der natürlichen Klangverwandtschaften, die meine C-Dur-Tonleiter aufweist – wäre ich schon mit dem ersten Tonschritt gescheitert, weil ich mit einer „falsch“ intonierten Sekunde beginnen müsste. Ich müsste einen neuen, passenden Ton e definieren.
Man muss also dafür sorgen, dass man einheitliche Tonschritte hat, die man dann (wenigstens in Maßen) auch auf andere Tonleitern transponieren kann. Das wusste schon Pythagoras, und er löste das Problem auf seine Weise. Das ganze Mittelalter hindurch galten die Stimmungsvorschriften des weisen Griechen als Maßstab. Als sich dann die Musik weiterentwickelte, stieß die bis dahin geltende Stimmung mehrfach an ihre Grenzen. Was dann passierte, welche Probleme sichtbar wurden und wie diese gelöst wurden – davon mehr in der nächsten Folge!
Aus akkordeon magazin #62, Juni/Juli 2018





0 Kommentare