Der lange Weg zu unserem Musiksystem (Folge 1)
Der lange Weg zu unserem Musiksystem (Folge 2)
Der lange Weg zu unserem Musiksystem (Folge 3)
Die „gleichschwebende“ Stimmung unserer Tasteninstrumente deckt sich oft nicht mit den natürlichen Klangverwandtschaften. Aus den Naturklängen kann man aber kein funktionierendes Tonsystem bauen. Das war die Lehre aus den beiden vorangegangenen Folgen dieser Kolumne. Die vorliegende Folge zeigt, was im Laufe der Jahrtausende unternommen wurde, um ein stabiles, taugliches Stimmungssystem zu schaffen.
Text: Peter M. Haas
Mit Pythagoras fing alles an …
Naja, jedenfalls waren Pythagoras und seine Schüler die ersten, die hier in Europa – etwa 600 v. u. Z. – die grundlegenden Tonverwandtschaften definierten. (Ein fast identisches Tonsystem hatte es bereits 2000 Jahre vorher in China gegeben, es soll auf den Gelehrten und Weisen Konfuzius zurückgehen.)
Durch Experimente mit schwingenden Saiten und deren Länge, Dicke und Spannung ermittelte Pythagoras die Schwingungsverhältnisse der grundlegenden Intervalle:
- Ein Frequenzverhältnis von 1 : 2 ergibt die Oktave.
- Ein Frequenzverhältnis von 2 : 3 ergibt die Quinte.
- Ein Frequenzverhältnis von 3 : 4 ergibt die Quarte.
(Siehe Folge 1 dieser Kolumne)
Durch Verkettung dieser Verwandtschaften konnte man die übrigen Intervalle und ihre Frequenzen festlegen.
Was stimmt nicht bei Pythagoras?
Dieses Tonsystem, beruhend auf reinen Quinten und Quarten, hatte in Europa bis gegen Ende des Mittelalters Gültigkeit. Zwar hatten Schüler des Pythagoras längst schon die beiden Schwachstellen des Systems herausgefunden, das wusste aber in Europa niemand. Wieso nicht? Das Musikwissen der Griechen war im Mittelalter sozusagen nur aus zweiter Hand zugänglich, nämlich in der lateinischen Übersetzung des Gelehrten Anicius Boëtius. Dieser Autor hatte zwar die Intervallbestimmung in seine Übersetzung aufgenommen, nicht aber die Berechnungen der Pythagoras-Schüler.
Terzen sind verboten
Eigenartig im pythagoräischen System ist ja: Nur Quinten, Quarten und Oktaven sind als Konsonanz anerkannt. Von Terzen – ohne die wir keine Akkorde bilden können – ist nicht die Rede. Im Mittelalter störte das noch nicht, denn genau so musizierte man damals ja auch. Akkorde gab es nicht, nur strenge, leere Quart- und Quintintervalle.
Für Pythagoras hatte diese Beschränkung sicher auch philosophisch-dogmatische Gründe: Es lag ihm viel daran, zu zeigen und zu beweisen, dass das ganze Weltgefüge in wesentlichen Dingen durch einfachste Zahlen und ihre Verhältnisse strukturiert wird. Im Mittelalter verteidigte die Kirche diese Ordnung konsequent.
Fehlerfaktor 1: syntonisches Komma – reine Quinten contra Terzen
Es ging aber nicht nur um die Ideologie. Folgte man den Tonberechnungen des Pythagoras, erhielt man eine sehr unschön klingende Terz. Inzwischen wissen wir, dass der großen Terz (Durterz) ein Schwingungsverhältnis von 4 : 5 zugrunde liegt. Die Terz im pythagoräischen System weicht davon empfindlich ab.
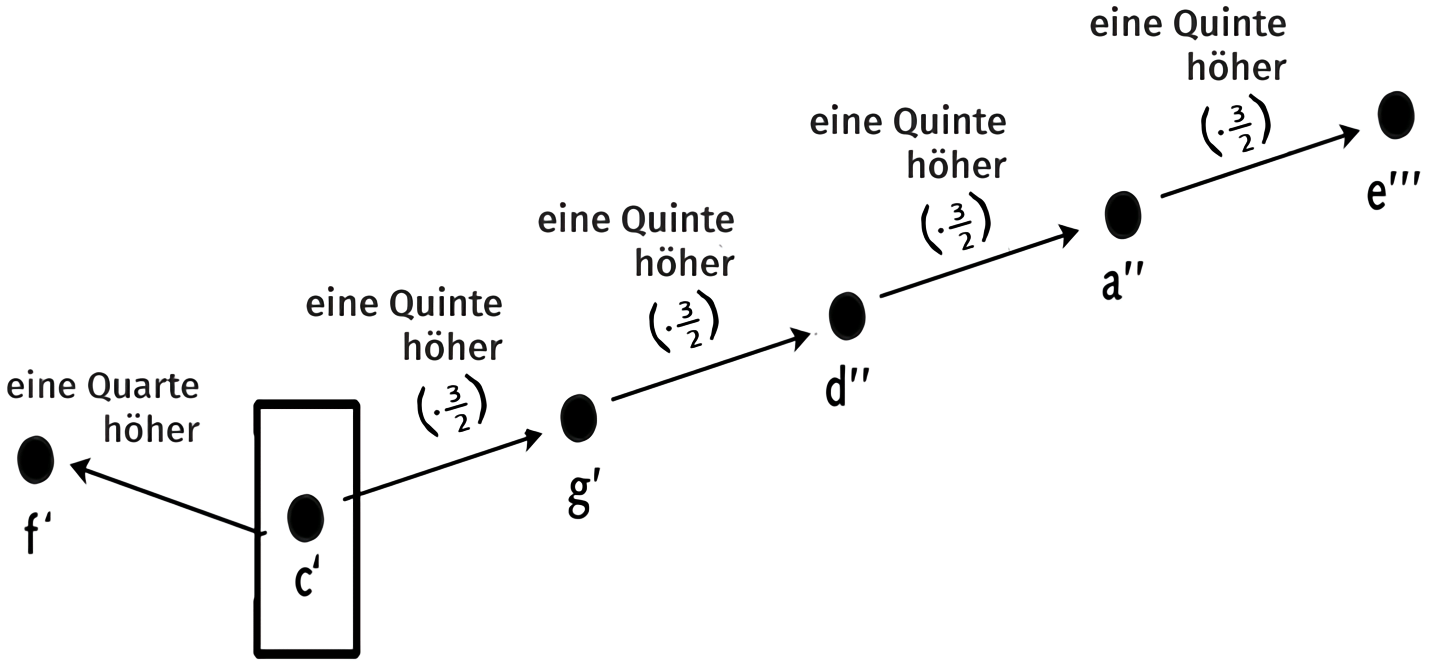
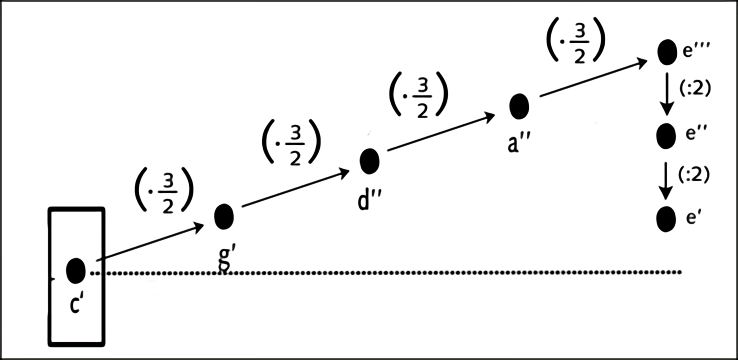
Ermittelt man die Terz nach der Rechnung des Pythagoras (vom c viermal eine Quinte hoch, danach wieder zwei Oktaven abwärts – ich habe es ganz fleißig nachgerechnet), erhält man nicht das Zahlenverhältnis 4 : 5. Man kommt vielmehr auf das Verhältnis 64 : 81, und der Vergleich zeigt:
pythagoräische Terz: 64:81
Abweichung (syntonisches Komma) 80:81
Den Unterschied zwischen der reinen Terz und der pythagoräischen Terz nennt man syntonisches Komma (80 : 81, das entspricht etwa 21 cent).
Das ganze europäische Früh- und Hochmittelalter hindurch war es kein Problem, der Stimmung des Pythagoras zu folgen: Die Musik benutzte keine Terzen. Erst gegen Ende des Mittelalters drängten die Musiker immer mehr dazu, Dreiklänge zu benutzen, also die Zusammenklänge Grundton – Terz (groß oder klein) – Quinte. Jetzt konnte man sich nicht mehr damit abfinden, dass große und kleine Terz Dissonanzen sein sollten; eine Neubewertung und Neuberechnung der Intervalle wurde gesucht. Gefragt war eine Stimmung, die einen Kompromiss fand zwischen reinen Terzen einerseits und gut klingenden Quinten andererseits.
Mitteltönige Stimmung
Das Bedürfnis nach gut klingenden Terzen zwang zu einem Kompromiss. Nun wussten die Instrumentenbauer bereits: Wenn ich eine Quinte ein kleines bisschen verstimme, nimmt sie der Hörer immer noch als sauber wahr. Daher ist es möglich, systematisch alle Töne so zu verstimmen, dass jede der Quinten c – g, g – d, d – a, a – e eine Idee zu klein ist. Damit hat man den Fehlerfaktor des syntonischen Kommas auf die vier Quinten verteilt (dabei wird jede nur um etwa 3,5 cent verstimmt) und erhält eine Terz c – e mit sauberem Schwingungsverhältnis.
Von diesem Gedanken ausgehend, verstimmte man in der mitteltönigen Stimmung die meisten Quinten so, dass die wichtigsten Terzen rein klingend benutzt werden konnten. Diese mitteltönige Stimmung, im Jahr 1523 erstmalig erwähnt, war die verbreitete Stimmung in Renaissance und frühem Barock. Dann stieß man aber auch bei dieser Stimmung an die Grenzen. Als das Bedürfnis wuchs, in vielen verschiedenen Tonarten zu spielen, war der nächste Fehlerfaktor im Weg: Das sogenannte pythagoräische Komma.
Fehlerfaktor 2:
das pythagoräische Komma – oder gis ist nicht gleich as
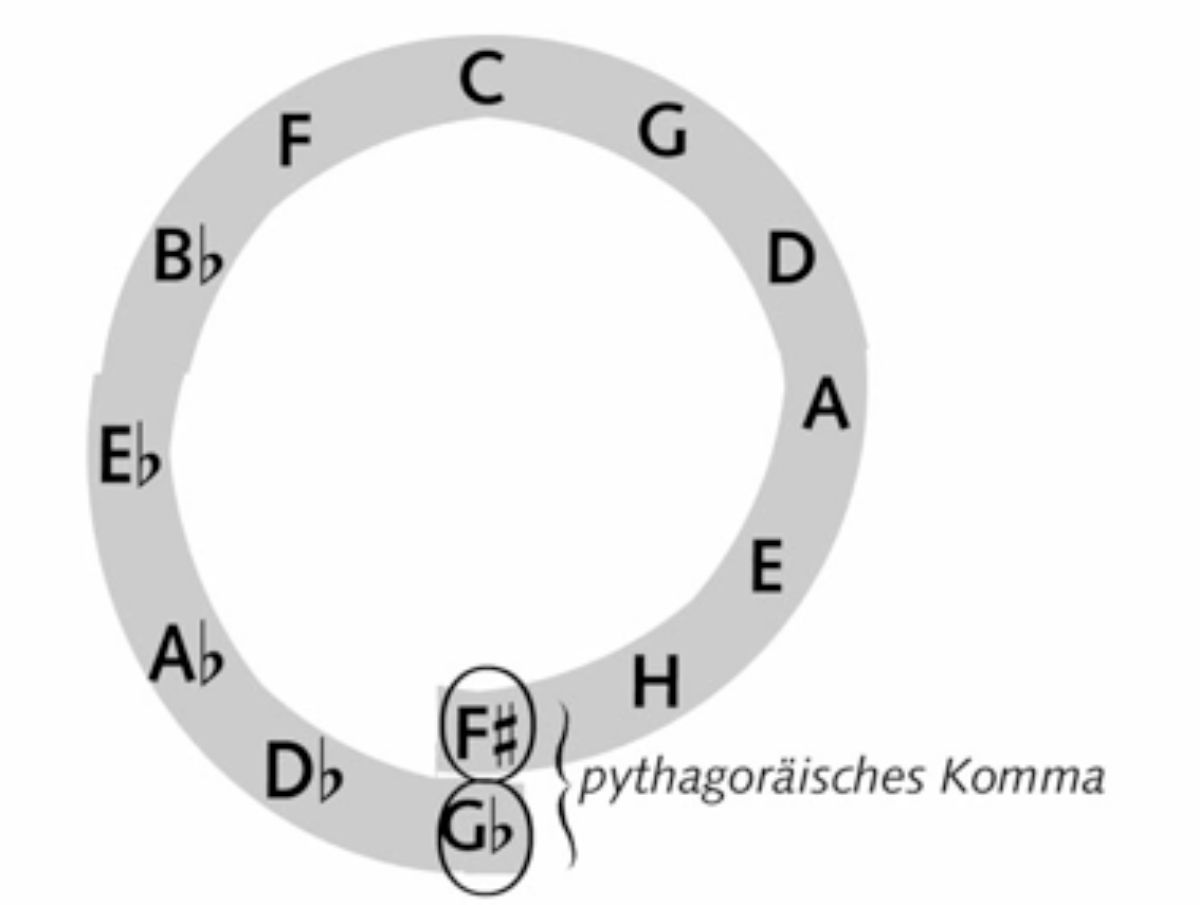
Ihr kennt alle das Bild vom Quintenzirkel, wie er in jedem Lehrbuch steht: Von c geht es lauter Quinten aufwärts, und wie durch ein Wunder landet man zum Schluss wieder bei C.
Das stimmt aber ursprünglich gar nicht. Schon einer der Schüler von Pythagoras hat berechnet: Gehe ich von C zwölf Quinten aufwärts, lande ich bei einem Ton, der sich von C deutlich hörbar unterscheidet. (In cent ausgedrückt, beträgt der Unterschied etwa 23 cent).
Unser heutiges Denken im Quintenzirkel setzt voraus, dass man erniedrigte Töne (= ges) und erhöhte Töne (= fis) gleichsetzen kann (sogenannte enharmonische Verwechslung). Das ist aber ein Luxus, der erst in der heutigen, gleichschwebenden Stimmung möglich wurde!
17 Töne pro Oktave?
Seit man in stärkerem Maße mit ♯ und ♭ arbeitete, war bekannt, dass die Oktave nicht zwölf, sondern 17 verschiedene Töne enthalten muss, nämlich diese:
| cis des | dis es | fis ges | gis as | ais be | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| c | d | e | f | g | a | h | c |
Als Erster gab im Jahr 1412 Prosdocimus de Beldemandus in seinem „tractatus de contrapuncto“ diese Ordnung der Töne an; den Unterschied zwischen den jeweils beieinanderliegenden, versetzten Tönen nennt er chroma. (Das entspricht dem pythagoräischen Komma.)
Wie behalf man sich in der Praxis? Ganz einfach – man durfte nicht zu viele ♯ oder ♭ verwenden. Zwei ♭ konnte man problemlos verwenden (B und Es), ebenso ♯♯ (fis und cis). Aber bei der verbleibenden schwarzen Taste musste man sich bereits entscheiden: Stimmte man sie als gis, konnte man in A-Dur spielen (♯♯♯), stimmte man sie als as, konnte man in Es-Dur spielen (♭♭♭). Entweder – oder: Beides ging nicht, zumindest nicht auf Tasteninstrumenten.
Instrumentenbauer versuchten eine Lösung. Aber die Tastatur, bei der die Tasten für es/dis und für gis/as in zwei kurze Tasten geteilt sind (siehe Abbildung), setzte sich nicht durch, was ich aus meiner Keyboarder-Praxis nur sehr begrüßen kann.
Oder besser doch 51 Töne pro Oktave?
Konnte man denn ein Musiksystem finden, das es erlaubte, rein klingend in allen Tonarten zu musizieren? Die Mathematiker des 18. Jahrhunderts nahmen sich das Problem vor, allen voran Leonhard Euler. Er schlug 1774 ein Tonsystem vor, das pro Oktave etwa 50 verschiedene Tonstufen hatte: Neben den oben gezeigten 17 Tönen auch noch (ein etwas höheres c, d, e …) sowie c , d , e … als etwas tiefere Töne.
Das „Wohltemperirte Clavier“
Für die praktischen Musiker auf dem Tasteninstrument war das natürlich keine besonders sinnvolle Lösung. Eine andere Idee bekam daher immer mehr Gewicht: Schon in der mitteltönigen Stimmung wurden ja die Quinten „temperiert“, d. h. geschickt in ihrer Stimmung verfälscht. Wie wäre es, wenn man noch konsequenter temperiert und den Fehlerfaktor des chroma gleichmäßig auf alle (bzw. zunächst einmal auf fast alle) Quinten verteilte?
Wer hat’s erfunden? Die Italiener!
Seit etwa 1500 wurden – vor allem in Italien – solche temperierten Stimmungen erprobt und diskutiert. Der Italiener Joseffo Zarlino gab bereits 1588 drei Arten an, die Oktave „direttamente in 12 parti o semituini eguali e proportionati“ [Riemann, Geschichte der Musiktheorie, Berlin 1921, S. 336)] zu teilen. In Deutschland wurden diese „wohltemperierten“ Stimmungen erstmals durch Andreas Werckmeister (1645 – 1706), Organist in Halberstadt, publiziert („Musikalische Temperatur“, 1691).
Johann Sebastian Bach benutzte als Erster diese neuartige Stimmung der Tasteninstrumente, als er sein „Wohltemperirtes Clavier“ (1722) schrieb: eine Sammlung von 24 Präludien und Fugen – in jeder der zwölf Dur- und zwölf Molltonarten jeweils ein Präludium und eine Fuge. Erstmals war es möglich, in jeder der Tonarten zu spielen.
In Werckmeisters wohltemperierter Stimmung waren noch nicht alle Tonschritte gleich. Werckmeister veröffentlichte mehrere unterschiedliche dieser wohltemperierten Stimmungen, bei denen er die Reinheits- und Unreinheits-Kompromisse unterschiedlich verteilte. Komponisten wie Bach benutzten diese Klangunterschiede in ihren Kompositionen, indem sie schlechter gestimmte Akkorde als verdüsternde Effekte einsetzten.
Gleichschwebende oder gleichstufige Stimmung
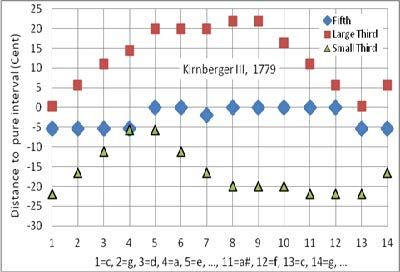
Noch in der Zeit nach 1760 arbeitete der Klavierbauer und Bach-Schüler Johann Philipp Kirnberger daran, andere Arten der Temperierung zu entwickeln. Mehr und mehr setzte sich dann aber die gleichstufige Stimmung durch.
In der gleichschwebenden oder gleichstufigen Stimmung sind alle Unterschiede konsequent beseitigt. Alle Halbtonschritte sind hier exakt gleich:
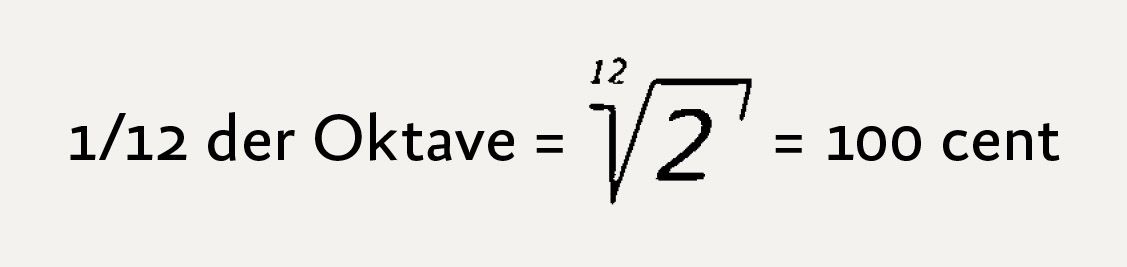
Halbtonschritte
aus »Der lange Weg zu unserem Musiksystem)«, Bild: Peter M. Haas
Immer wieder gab es gegen diese Stimmung Einwände. In der ersten Folge unserer Kolumne habe ich ja davon berichtet, dass Orchestermusiker anderer Instrumente keineswegs „wohltemperiert“ spielen – mein Freund, der Konzertgeiger, spielt sein fis anders als sein ges und muss diese Unterschiede bewusst verflachen und verwässern, wenn er mit Tasteninstrumenten zusammenspielt. Musik aus der Renaissance wird auch heute noch bevorzugt mit mitteltönig gestimmtem Cembalo aufgeführt. Die entlegenen Tonarten (As-Dur, Des-Dur, E-Dur …) sind dann nicht spielbar, aber sie kommen in der Musik dieser Epoche ja auch noch nicht vor. Dafür klingen die Harmonien der gängigen Tonarten ausgewogener – jedenfalls für den sehr genau auf die Klänge achtenden Hörer.
Reiner Klang aus dem Rechner?
Trotz aller Einwände hat sich die gleichschwebende Stimmung – als alltagstaugliche Kompromisslösung – in der Praxis durchgesetzt. Sie ist damit der Endpunkt einer langen Suche nach einem optimalen Stimmungssystem.
Moment mal – ist sie wirklich der Endpunkt? Mit den Composer-Programmen und digitalen Keyboards (bei allen ihren entsetzlichen Nachteilen) haben wir doch ganz neue Möglichkeiten! Wäre es nicht möglich, jetzt jeder Tonart, jedem Akkord die bestklingenden Intervalle zuzuweisen? Kann man der langen Suche dann vielleicht ein neues, letztes Kapitel hinzufügen?
Für mich war es eine Überraschung zu erfahren: Dieses letzte Kapitel ist längst geschrieben. Durch Zufall – und auf der Suche nach einer Software, mit der ich ein Klangbeispiel in Renaissance-Stimmung aufnehmen könnte – fand ich beim Googeln das Stichwort „Hermode-Tuning“. Tatsächlich ist das eine Stimmung, in der die Software die gerade geltende Tonart und den gerade geltenden Akkord analysiert und auf dieser Basis die Töne der gleichschwebenden Stimmung um die nötige Anzahl cent nach oben oder unten korrigiert.
Eine „klammheimliche“ Revolution
Wie kommt man an dieses Tuning heran? Die nächste Überraschung: Die großen Musikprogramme wie Logic, Cubase und Capella haben es schon vor Jahren implementiert, eigentlich eher „heimlich, still und leise“. (Bei Logic muss beispielsweise der fortgeschrittene Benutzer „Einstellungen > Erweiterte Werkzeuge einblenden“ wählen, damit die Wahlmöglichkeit überhaupt sichtbar wird.) Native Instruments, die Hersteller vieler virtueller Instrumente, prüfen gerade den Einsatz für ihren Kontakt-Player. Die Hersteller von Digitalpianos haben bisher noch kein Interesse gezeigt, aber es gibt die erste echte Pfeifenorgel mit Hermode-Tuning. Bei dieser werden die Pfeifen mittels Magnetantrieben und passenden Stimmeinrichtungen quasi in Echtzeit nachgestimmt. Sie ist in der Taufkirche von Martin Luther in Eisleben zu finden.
Eine digitale Kirchenorgel mit Hermode-Tuning gibt es als Prototyp; auf YouTube findet man ein interessantes Video über dieses Instrument und seinen Klang ( https://www.youtube.com/watch?v=uHIA-DM3Wrs ). Dort wird auch die Gegenüberstellung von temperierter Stimmung und der Bereinigung durch das Hermode-Tuning vorgeführt.
Wer hat’s erfunden? Ein Schwabe!
Wer hat dieses Tuning erfunden? Es ist der Musiker Werner Mohrlok, der seine Firma in Trossingen hat. Er ist nicht Programmierer und nicht Musikwissenschaftler, sondern aktiver Musiker. Als Fagottist spielte er in Orchestern und Kammermusik-Ensembles. Sein Interesse zur Entwicklung seiner Erfindung war ganz praktisch: Er übt seine Parts zu Hause zu Orchester-MIDI-Dateien. Diese werden natürlich üblicherweise vom Rechner in gleichschwebender Stimmung abgespielt, was ihn behinderte – er wollte ja beim Üben richtig, also orchestertreu untemperiert intonieren.
Wie das Tuning genau funktioniert, erklärt er auf seiner Webseite. Die ist ohnehin sehr zu empfehlen: Zur Entwicklungsgeschichte der musikalischen Stimmungen gibt Mohrlok einen genauen Abriss, der mit vielen vergleichenden Hörbeispielen belegt ist: www.hermode.com
Mit diesen Erklärungen und Hörbeispielen könnt ihr das Thema zum Abschluss unserer Kolumne noch einmal vertiefen.
Damit, liebe Leser, ist unser Streifzug durch die Geschichte der musikalischen Stimmung beendet. Ihr habt mitbekommen, dass ich versucht habe, allzu viel Mathematik zu vermeiden, ganz weglassen konnte ich sie aber nicht. Meine nächste Kolumne wird mit Sicherheit weniger theorielastig sein. Ich hätte da schon eine Idee für’s nächste Heft …
Bis bald! Euer Peter M. Haas
Aus akkordeon magazin #63, August/September 2018






0 Kommentare